Восстановление ансамбля аквахлоридных комплексов Pt(II). Анализ в рамках феноменологического подхода.

И.В.Побелов, М.И.Борзенко, Г.А.Цирлина, О.А.Петрий

Московский государственный университет им. М.В.Ломоносова

Предложен общий подход к феноменологическому анализу экспериментальных данных по кинетике электродной реакции, осложненной быстрыми предшествующими химическими стадиями. Возможности подхода, основанного на рассмотрении зависимости скорости процесса при постоянном заряде электрода от концентрации электролита фона, проиллюстрированы на примере реакции восстановления лабильных хлоридных комплексов Рt(II) в присутствии хлоридного, индифферентного (в смысле внутрисферного замещения) и смешанного электролитов фона. Проведенный анализ обобщает соотношение Фрумкина — Петрия, которое в отсутствие предшествующих стадий определяет средний заряд реагента в объеме раствора. При наличии в системе ансамбля реагентов аналогичные соотношения учитывают наряду с объемными свойствами системы также строение межфазной границы и отношения парциальных констант скорости параллельных реакций с участием реагентов разной зарядности.
 

В настоящей работе предпринята попытка проанализировать кинетические закономерности одновременного восстановления ансамбля квадратных комплексов Pt(II) — тетрахлоридного комплекса и продуктов его частичного гидролиза, моно- и диаквазамещенных комплексов. Целью анализа является отнесение определяемых параметров к конкретной реагирующей частице и/или ее локализации в реакционном слое. Электровосстановление PtCl₄^2– на ртутном электроде исследовалось ранее в [3–7] (а также менее подробно в более ранних работах, цитируемых в [3–7]) в присутствии хлоридных электролитов фона разных концентраций (с). В области отрицательных зарядов поверхности s были зарегистрированы [6,7] значительные эффекты торможения процесса даже при концентрации КСl > 1 М, не вполне типичные для реакций восстановления анионов. При последующем рассмотрении данных [6,7] в [8] обсуждалась возможность гидролиза по первой ступени, степень которого уменьшается с ростом [Cl^–]. Однако количественный анализ равновесий в объеме раствора был затруднен отсутствием надежных термодинамических и кинетических данных по гидролизу хлоридных комплексов Рt(II). Результаты, относящиеся к влиянию концентрации хлорида на электровосстановление Рt(II) на положительно заряженной поверхности ртути [4,5], а также на восстановление Рt(II) на платиновом электроде [9,10], вряд ли можно непосредственно сопоставлять с данными [6,7], поскольку в указанных системах имела место специфическая адсорбция хлорид-ионов.

Другой возможной причиной аномального хода полярограмм в растворах PtCl₄^2– + КСl, схематически рассмотренной в [11], является изменение соотношения различных ориентаций реагента (увеличение доли вертикально ориентированных частиц с ростом отрицательного заряда электрода). При этом расстояние тунелирования электрона вовзрастает и вероятность его переноса уменьшается. Ориентационно-зависимыми кинетическими параметрами являются энергии подвода реагента и отвода продукта, энергии реорганизации растворителя, а также трансмиссионный коэффициент, причем такого рода зависимостей можно ожидать как для исходного комплекса, так и для аквазамещенных. Однако детальное рассмотрение микроскопики реакционного слоя требует предварительной характеристики системы в широком интервале объемных составов и усовершенствования феноменологического анализа полярограмм.

В настоящей работе проведены сравнительные исследования кинетики восстановления ансамблей квадратных комплексов Рt(II) в растворах равновесного и неравновесного составов с разными концентрациями хлоридного, нитратного и перхлоратного электролитов фона (в том числе со смешанными хлоридно-перхлоратными фоновыми электролитами). Рассмотрена в общем виде задача о зависимости плотности кинетического тока  j концентрации фона для произвольного числа ступеней гидролиза и модифицировано на этой основе уравнение Фрумкина — Петрия [2,8]. Показано, что отклонения определяемой по методу Фрумкина — Петрия величины производной от величины среднего заряда в объеме раствора могут быть использованы в условиях одновременного восстановления нескольких частиц разной зарядности для оценки парциальных кинетических параметров.

Спектры поглощения регистрировали при температуре 25±0,5 ^оС при помощи прибора Hitachi 150–20 в спектральном диапазоне 280–500 нм, помещая в кювету сравнения фоновый раствор.

Использовали дважды перекристаллизованные из бидистиллата соли, растворы готовили на бидистиллированной воде и деаэрировали аргоном, очищенным от следов кислорода на медь-хромовом катализаторе.

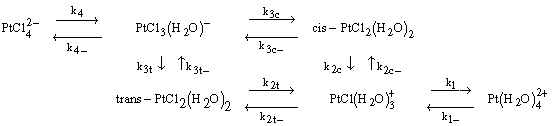
Оценки по данным Таблицы 1 (номера реакций в ней соответствуют вышеприведенной схеме и обозначены в сооответствии с общепринятыми) показывают, что за время около 100 мин (от момента приготовления растворов до начала полярографических исследований, с учетом времени деаэрирования) составы растворов, использованных в [5,6], оказывались еще достаточно далеки от равновесных.

Последнее подтверждается спектрами поглощения (рис 1 , рис 2): эволюция полос поглощения продолжается сотни и тысячи минут.

Коэффициенты экстинкции для приведенных на рис. 1,2 полос поглощения (»325 и »385 нм) близки к данным [21], а тенденция к увеличению поглощения в области 380–400 и его уменьшению в области 380–400 нм в ходе гидролиза согласуется с наблюдаемым в [21]. Для слабой полосы при »480 нм, которую ранее регистрировали только в [15], существенной зависимости интенсивности от времени не наблюдается.

Спектрофотометрически различимая зависимость от времени исчезает в течение 100 мин только для раствора с добавкой 1 М КСl. Спектры измеряли в основном для растворов с концентрацией К₂РtCl₄ (C), превышающей используемые в полярографических опытах в 5–10 раз (с целью обеспечения достаточной чувствительности). Это, однако, могло привести только к переоценке времени достижения равновесия, но не наоборот.

С использованием приведенных выше величин К и k для 25 ^oС были рассчитаны долевые концентрации частиц в растворах c C = 0.5 мМ и разными добавками хлорид-ионов (Таблица 2) для характерных времен полярографирования свежеприготовленных растворов и равновесного состояния. Для растворов без добавок хлорида данные таблицы можно рассматривать как количественные только в случае равновесных составов, которые достигаются при t не менее 10 000 мин., поскольку в расчете кинетики гидролиза вводилось допущение неизменности концентрации хлорида, которое в данном случае нарушается.

В растворах с исходной концентрацией К₂PtCl₄ не менее 1 мМ даже в присутствии хлоридного фона, а тем более в отсутствии добавок КСl нельзя игнорировать, с учетом величин в Таблице 2, протекание процессов гидролиза по первой и второй, а возможно и по третьей ступеням. Таким образом, ансамбль реагентов включает (N+1) = 4 типа частиц разной зарядности (0 £ i £ N).

Роль ориентации реагирующих частиц на межфазной границе в исследуемой системе будут рассмотрены в специальном сообщении. Здесь отметим только, что поскольку для каждой из форм реагента, имеющей определенное молекулярное строение и распределение электронной плотности, ориентационные зависимости энергии реорганизации и предэкспоненты являются достаточно плавными, следует ожидать преобладающего вклада сравнительно узкой части углового распределения, в первом приближении — одной фиксированной ориентации. В то же время оптимальный угол между плоскостью реагента и электрода для частиц разной зарядности может заметно отличаться, что в рамках предложенного в [11] микроскопического анализа псиприм-эффектов формально соответствует различию плоскостей локализации эффективных точечных реагентов разной зарядности. Характеризуя такие плоскости для каждой i-ой формы потенциалами (y_x)_i, долю реагента с зарядом (z – i) в реакционном слое можно представить как
           (1)
(где с_i — безразмерная объемная доля, Табл. 2). Зависимости с`_i от потенциала для разных концентраций электролита фона представлены на рис. 3(а,б, в). Кривые на рис. 3(а – в) построены в простейшем предположении y_x  = y₀   для любого i (y₀  — потенциал внешней плоскости Гельмгольца, здесь и далее используется по данным [22]).

На первый взгляд может показаться, что при малых концентрациях электролита фона (а, следовательно и ощутимых количеств продуктов глубокого гидролиза) при большом отрицательном заряде поверхности в реакционном слое велики относительные концентрации катионных форм PtCl(H₂O)₃⁺ и Pt(H₂O)₄²⁺. Однако результаты, полученные при более детальном рассмотрении реакционного слоя (с учетом микроскопического строения реагентов) говорят о том, что работы приближения всех катионных форм реагента меньше по абсолютной величине, чем рассчитанные в рамках точечного приближения (т. е. как притяжение катионных форм, так и отталкивание анионных выражены слабее, чем для точечных зарядов). Микроскопические эффекты строения реакционного слоя будут рассмотрены в отдельном сообщении, здесь же укажем, что для учета этого результата мы должны формально приписать катионным формам меньшие эффективные заряды (+(0.6–0.7) вместо +1 и +(1.2–1.4) вместо +2 для самых выгодных ориентаций). Отклонение от формальной величины заряда усиливается при смещении в сторону более отрицательных потенциалов. При этом вклад Pt(H₂O)₄²⁺ становится меньше, чем вклад незаряженной формы, а вклад PtCl(H₂O)₃⁺  гораздо меньше обоих этих величин (рис 3г). В связи с вышеизложенным при рассмотрении данных настоящей работы рассматривается кинетическое уравнение для N = 2 (три электрохимически активных частицы).

Различия полярограмм в «нитратной» и «перхлоратной» сериях проявлялись только в области Е отрицательнее минимума (при потенциалах тем более отрицательных, чем меньше была величина с) и были обусловлены вкладами токов восстановления нитрат-аниона. Хорошее совпадение данных для с = const в нитратных и перхлоратных растворах в области спадов и минимумов тока свидетельствует об индифферентности кислородсодержащих анионов в отношении внутрисферной ассоциации с реагентом. Для стандартизации условий старения растворов применяли режим, предложенный в [19] — выдержку на водяной бане при температуре 60^о С в течение 48 ч. Это, как можно заключить из контрольных спектров, заведомо обеспечивало равновесные составы для «хлоридной» серии и, по-видимому, лишь квазиравновесные для остальных растворов. Однако более длительное старение в отсутствие избытка хлорид-ионов приводило к снижению предельного диффузионного тока в области –Е = 0.8–1.0 В
(кривые 1'–4' рис. 4 а–в), что могло быть результатом частичного диспропорционирования Рt(II) при повышенной температуре.

Закономерности диспропорционирования Рt(II) детально не исследованы. Возможная роль явления диспропорционирования в кинетике электродных процессов с участием комплексов Рt(II) и Pt(IV) обсуждалась в [23], где дан обзор ранних работ. Предположения [23] оспаривались, однако, в [5], на основе возможных альтернативных объяснений сложных кинетических закономерностей в условиях химического взаимодействия Рt(II) со ртутью при положительных зарядах поверхности. Отметим, что независимые косвенные данные в пользу существенного диспропорционирования Рt(II) в хлоридных растворах за времена порядка десятков часов дают недавние результаты [24].

Однако вне зависимости от причин наблюдаемых осложнений можно однозначно утверждать, что увеличение степени и глубины гидролиза при старении обеспечивает резкое увеличение токов при с = const. В отсутствие добавок хлорида (кривые 1'–4' рис. 4 б , в) торможение в области –Е = 1.0–1.6 В оказывается тем меньше, чем выше с, а при с = 1 М фиксируется предельный диффузионный ток. Таким образом, в состаренных нитратных и перхлоратных растворах полярографическое поведение системы типично для реакций восстановления таких анионов, как, например, S₂O₈^2–.

В то же время в присутствии хлорид-ионов наблюдается немонотонная зависимость от с (кривые 1'–4' рис. 4а) : при увеличении с до 0.1 М торможение усиливается, а при с = 1 М лишь немного ослабляется. Такую зависимость в рамках электростатического рассмотрения эффектов торможения можно объяснить только в предположении о значительных различиях констант скорости реакций восстановления комплексов разной зарядности.

Количественную обработку данных, полученных в состаренных растворах, проводили только для заведомо равновесной «хлоридной» серии. Использовали также квазиравновесные данные для раствора без электролита фона в интервале потенциалов минимума, в котором они были наиболее воспроизводимы. Из зависимостей кинетических токов от концентрации электролита фона сечениями при [Е – (RT/F)lnc] = const (что эквивалентно в обсуждаемом интервале Е постоянству заряда s определяли производные  (некоторые примеры даны на рис. 5).

Предварительно было показано, что использование для построения сечений условия постоянства [Е – (RT/F)ln g_±c)] = const, где g_± — средний коэффициент активности, не приводит к изменению величин производной в пределах достигаемой точности. Погрешность расчета определяется в основном точностью введения поправки на концентрационную поляризацию, а также малым числом исследованных в каждой серии растворов с разными с.

Качественно полученные зависимости близки к построенным в [8] по данным [6,7]. Существенной особенностью —   , с-зависимости для состаренных хлоридных растворов является смена знака производной. Все полученные величины существенно отличаются от среднего заряда в объеме раствора  (Таблица 1). С целью установления причин этих отличий в следующем разделе рассмотрены особенности уравнения Фрумкина — Петрия для процессов многостадийного гидролиза.

Из соотношений для стадийных констант гидролиза К при условии с >> C, если электролит фона участвует в комплексообразовании, можно выразить объемную концентрацию каждой из форм как
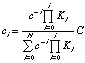,  (3)
и, соответственно, получить соотношение для среднего заряда в объеме раствора:
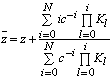(4)
При не слишком малых по абсолютной величине зарядах поверхности s и не слишком больших расстояниях от внешней плоскости Гельмгольца х [4] для любого i зависимость (y_x)_i от с имеет вид
(5)
для s <0 или
(6)
для s > 0^*.

Обозначение у_i введено для удобства дальнейшей записи и, в соответствии с уравнениями (5) и (6) характеризует величину потенциала y_x в растворе единичной концентрации. Подставляя (5) и (6) в (2), логарифмируя полученное выражение и дифференцируя затем его по lgc при постоянном s, имеем для отрицательных и положительных зарядов поверхности соответственно:
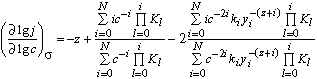   (7)
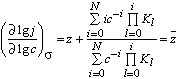            (8)
Выражения (7) и (8) схожи с полученными в [25] уравнениями (9) и (8) соответственно для ансамбля внешнесферных ассоциатов (с учетом того, что в [8] z определен как заряд по абсолютной величине аниона, вступающего в ассоциацию с катионами, по абсолютной величине, константы К характеризуют устойчивость ассоциатов, а вместо величины у использовано выражение через const). Прослеживаются, однако, два существенных отличия результатов [25] от уравнений (7), (8):
1) сходные ситуации — независимость или зависимость производной в левой части уравнения от k и у имеют место при противоположных знаках заряда поверхности;
2) знаки производных, соответственно, изменяются на противоположные (например, в [25] обсуждаемая производная равна среднему заряду в объеме раствора с противоположным знаком для отрицательно заряженной поверхности, а в уравнении (8) — с тем же знаком, но, соответственно, при положительном заряде поверхности).

Если все К стремятся к нулю (в [25], соответственно, к бесконечности), то есть в растворе преобладает единственная форма реагента (i=0), все обсуждаемые выражения сводятся к результату [2] (–z и z для отрицательно и положительно заряженной поверхности соответственно).

Вывод о симметрия рассмотренной задачи может быть сформулирован следующим образом: если с ростом концентрации участвующих в комплексообразовании ионов электролита фона средний заряд в объеме раствора (с учетом знака) убывает, то при s > 0 величина  равна  , а при s < 0 соответствует уравнению (7), вне зависимости от знака заряда z (i=0) и заряда фонового иона, участвующего в комплексообразовании. Если же, напротив, с ростом с  возрастает, то при s < 0 производная  равна , а на положительно заряженной поверхности — выражению в правой части (8), но с противоположным знаком.

При этом в приближении точечных реагентов (т.е. если каждой из форм в ансамбле приписывается эффективная плоскость локализации) процессы внешне- и внутрисферной ассоциации неразличимы. К первой группе процессов относятся, в частности, гидролиз комплексов с монодентатными анионными лигандами и образование внешнесферных ассоциатов редокс-активных катионов с анионами фона, ко второй — образование анионных ассоциатов с катионами фона и процессы протонирования (см. ниже).

Для внутрисферных процессов возможно также увеличение с путем введения фонового электролита, не обладающего способностью к комплексообразованию. Эта ситуация экспериментально реализованна в настоящей работе на примере «нитратной» и «перхлоратной» серий. Величины с_i оказываются в данном случае независимыми от с (или слабо изменяющимися с с вследствие зависимости К от ионной силы раствора). В первом случае для гидролиза комплексов с анионными лигандами из (3) получим для отрицательно и положительно заряженной поверхности соответственно
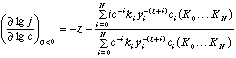(9),
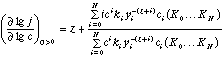(10)
то есть в любом случае зависимость тока от с определяется наряду с объемными свойствами системы также и парциальными константами скорости и строением двойного слоя. В общем случае с_i могут зависеть от ионной силы раствора и, соответственно, от с, но значительно слабее, чем в случае внутрисферного замещения анионом фона. Аналогичные (9) и (10) соотношения (с симметричной заменой знаков) справедливы для процессов, осложненных протонированием, в растворах с добавками индифферентного электролита фона (см., например, [26]).

Наконец, для внутрисферных ассоциатов возможен случай постоянства ионной силы (и потенциала в заданной плоскости локализации реагента) при переменной концентрации индифферентного электролита (некоторые экспериментальные данные [4,5,9,10] для кислых сульфатно-хлоридных растворов отвечают именно этой ситуации). Расчет величины  при этом одинаков для обоих знаков s и не требует выполнения условий (5) и (6), вместо которых достаточно записать  (y_x)_i = (RT/F)lng_i (при суммарной единичной концентрации фона g_i = y_i). Дифференцируя соответствующее уравнение для суммарной плотности тока, получим
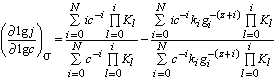(11)

Как видно из сопоставления уравнений (7), (9) и (11) (или (8), (10) и (11) при s > 0), в общем случае данные для растворов с хлоридным, индифферентным и смешанным электролитами фона обеспечивают независимую информацию о соотношениях величин k_i.

Надежность количественного сопоставления с экспериментом определяется точностью дифференцирования lgj, lgc — зависимостей, которая, в свою очередь, зависит от точности расчета величин  j путем введения поправки на концентрационную поляризацию. Не менее важно обеспечить точность расчета величин, зависящих от объемных свойств системы. Это можно более корректно сделать для равновесных составов растворов, поскольку величины констант скорости гидролиза менее надежны, чем величины равновесных констант К. Вследствие перечисленных обстоятельств мы вынуждены ограничиться рассмотрением только двух серий данных для состаренных растворов («хлоридной» серии, кривые 1`–4` рис. 4а, и серии со смешанным электролитом, кривые 1`–4` рис. 6) — в случае кривых 1`–4` рис. рис. 4б и рис. 4в токи во всем исследованном интервале близки к предельным, и точность расчета j безусловно недостаточна. По такой же причине из рассмотрения исключаются сечения  j,E-кривых в области начала спада тока.

Полученные зависимости lgj от lgc при постоянном заряде поверхности слабо зависят от потенциала. Среднее значение и отклонения от него были оценены по распределению Стьюдента (в качестве поправочного коэффициента  t_P,N брали 3 (при доверительной вероятности P=0.95 и N ³ 4 коэффициенты Стьюдента меньше этого значения). При этом отклонение от среднего значения для lgj оказалось равным 0.1–0.4. Соответствующий разброс в значениях производных равен 0.1–0.7.

Ниже будем рассматривать уравнения (7) и (11) (они описывают «хлоридную» серию и серию с постоянной концентрацией фона соответственно), введя соотношения k = k₀/k₂, k` =  k₁/k₂, то есть пронормировав все парциальные константы скорости на константу для нейтрального диаквакомплекса.

Из экспериментальных величин  c использованием значений констант гидролиза можно рассчитать зависящие от потенциала и парциальных констант скорости слагаемые уравнений (7) и (11) D₁ и D₂ соответственно):
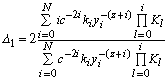(12)
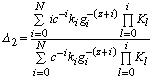(13)
Сопоставление полученных величины с модельными зависимостями для разных сочетаний параметров k и k` показывает, что чувствительность D<sub>1</sub> и D<sub>2</sub> к указанным параметрам достаточно высока. В частности, экспериментально наблюдаемые D<sub>1</sub>; получаются только при k` = 30–100 и k < 1–3 (рис. 7). Еще более жесткие ограничения накладывает сопоставление с величинами D₂, причем интервалы k, k`, отвечающие согласию с обеими независимыми экспериментальными величинами практически не перекрываются, а лишь соприкасаются. На этой основе можно оценить наиболее реалистичные значения как D₁ = 1 и D₂ = 100 (рис 8.).
 Для аналогичной оценки констант k_i, проведенной с учетом вклада PtCl(H₂O)₃⁺ (N=3) согласие теоретических кривых с экспериментальными данными наблюдается только при k₃/k₂ < 0.01, поэтому можно заключить, что наше допущение об участии в реакции только трех электрохимически активных форм является достаточно разумным.

Особенно неожиданно обоснованное выше предположение о том, что константа скорости восстановления PtCl₃(H₂O)^– существенно выше, чем для восстановления PtCl₄^2– и PtCl₂(H₂O)₂. Этот результат требует количественного анализа электронного перекрывания, который мы предполагаем выполнить в дальнейшем.

В первую очередь ответственными за различия в величинах парциальных констант восстановления являются, по-видимому, различия в строении акцепторных орбиталей комплексов разного состава и специфика механизмов процесса (перенос электрона с разрывом связи или без разрыва, с участием или без участия мостиковых атомов, с образованием адсорбированных интермедиатов и т.п.). Не исключено также различное адсорбционное поведение обсуждаемых частиц разной зарядности. Это обстоятельство существенно, поскольку выше рассмотрение работ сближения реагентов сводилось только к учету электростатических составляющих, а энергии адсорбции реагентов и продуктов были включены как составляющие энергии активации в величины k).

Необходимо подчеркнуть, что все рассмотренные выше соотношения для  представляют в компактной форме теорию замедленного разряда для стадийных процессов с быстрой химической реакцией, предшествующей переносу электрона. В этом смысле предложенный подход не противворечит традиционному рассмотрению подобных реакций [27].

Полученные соотношения сохраняют силу и при рассмотрении зависимостей плотности тока от потенциала в соответствии с теорией Маркуса и квантово-механической теорией элементарного акта переноса электрона (см. сравнительный анализ в [28]). При этом возможные различия коэффициентов переноса для разных реагентов ансамбля в рассматриваемых интервалах перенапряжений эффективно входят в формальные величины k_i. Очевидно, однако, что при любых перенапряжениях основными факторами, определяющими более высокие k_i, являются высокие значения парциальных трансмиссионных коэффициентов и низкие энергии реорганизации (даже если в области высоких перенапряжений происходит заметное снижение коэффициентов переноса).

Анализ, проведенный в настоящей работе, не учитывал возможности образования катион — анионных ассоциатов на основе  PtCl₄^2– и PtCl₃(H₂O)^–, которую в принципе нельзя исключить при высоких концентрациях фона. Однако для квадратных комплексов такая ассоциация выражена, по-видимому, сравнительно слабо [29]. Специальное рассмотрение эффектов анион-катионной ассоциации в присутствии в растворе ансамбля анионов предполагается выполнить в дальнейшем. На качественном уровне однако, можно сказать, что снижение по абсолютной величине зарядов всех (в том числе и катионных) форм реагента приведет к перераспределению реагентов в реакционном слое в пользу анионных форм и расширит диапазон концентраций, в которых вклад катионных форм можно не учитывать.

Работа выполнена в рамках проекта РФФИ 99–03–32367а. Авторы признательны проф. В.И.Кравцову за многочисленные советы и ценное обсуждение.

Форма реагента	с=1 t=90	t=¥	с=0.1 t=90	t=¥	с=0.01 t=90	t=¥	с=0 t=90	t=¥
PtCl42–	98.73	98.73	90.64	88.46	83.51	40.13	»10–3	1.49
PtCl3(H2O)–	1.27	1.27	9.29	11.37	15.52	51.59	»10–3	26.1
cis-PtCl2(H2O)2	»10–3	»10–3	0.07	0.09	0.97	4.13	»10–3	28.43
trans-PtCl2(H2O)2	»10–4	»10–3	»10–3	0.07	»10–3	4.08	»10–3	34.46
PtCl(H2O)3+	»10–8	»10–3	»10–6	»10–4	»10–3	0.08	»10–3	9.39
Pt(H2O)42+	»10–13	»10–3	»10–10	»10–8	»10–3	10–4	»10–3	0.13
Средний заряд	–2	–2	–1.9	–1.88	–1.83	–1.32	±–1.8	–0.19

Рис. 2. Спектры поглощения раствора 5*10^–3 M K₂PtCl₄ + 10^–2 M NaNO₃; время после приготовления раствора, мин: 1 — 1, 2 — 104, 3 — стационарное состояние.

Рис. 3. Относительные концентрации в реакционном слое, рассчитанные по уравнению (1), для следующих форм реагента: 1 — PtCl₄^2–, 2 — PtCl₃(H₂O)^– , 3 — cis-PtCl₂(H₂O)₂, 4 — trans-PtCl₂(H₂O)₂, 5 — PtCl(H₂O)₃^– , 6 — Pt(H₂O)₄²⁺. Концентрация электролита фона, М: 1 (а), 0.1 (б), 0.01 (в), 0.01 в микроскопическом рассмотрении (г). Общая концентрация комплекса 5 мМ.

Рис. 4. Полярограммы восстановления 0.5 мМ K₂PtCl₄, полученные для следующих концентраций электролита фона, М: (1,1`) — 0, (2,2`) — 9(10–3), (3,3`) — 0.1, (4,4`) — 1; 1–4 — свежеприготовленные растворы; 1'–4' — состаренные растворы. Электролит фона: KСl (а), NaNO₃ (б), KClO₄ (в).

Рис. 5. Производные , рассчитанные из кривых 1`–4` рис. 4а при фиксированных [Е – (RT/F)lnc]: 1 — (–1.02), 2 — (–1.17), 3 — (–1.27), 4 — средний заряд в обьеме раствора (Таб. 2).

Рис. 6. Полярограммы растворов со смешанным электролитом, полученные для суммарной концентрации 10^–2 М. Концентрация KCl, М: (1,1`) — 0, (2,2`) — 0.001, (3,3`) — 0.01, (4,4`) — 0.1; 1–4 — свежеприготовленные растворы; 1'–4' — состаренные растворы.

Рис. 7. Области значений k; и k`, отвечающие согласию величин D₁ и D₂, определенных из экспериментальных данных и расчитанных по уравнениям (12) и (13) соответственно. 1 — D₁,2 — D₂

 Рис. 8. Значения D₁; 1,2,3 — расчет из величин на рис. 5, 4 — по уравнению (12) при предпочтительных величинах k; и k`.

Back