Микроскопический подход к описанию реакции восстановления персульфат-иона на ртутном электроде

Р.Р. Назмутдинов, Д.В. Глухов, Г.А. Цирлина* и О.А. Петрий*

Казанский государственный технологический университет

*Московский государственный университет им. М.В. Ломоносова, Химический факультет

Аннотация

В рамках современной теории переноса заряда в полярных средах и квантовохимических подходов проведено моделирование поляризационных кривых электровосстановления S₂O₈^2- на ртутном электроде в области высоких перенапряжений для различных концентраций поверхностно-неактивного электролита фона. На основе анализа адсорбции реагента с использованием кластерной модели сделано заключение о локализации персульфат-иона в диффузной части двойного электрического слоя. При расчете тока предполагалось, что перенос первого электрона, сопровождающийся разрывом связи, является лимитирующей стадией суммарного двухэлектронного процесса.
Выполнено интегрирование по всему электронному спектру металлического электрода и сделана попытка учесть на молекулярном уровне электростатические и сольватационные эффекты, показано, что экспериментально исследованный интервал перенапряжений соответствует протеканию процесса в окрестности безактивационной области. При этом рост тока при высоких отрицательных зарядах поверхности обусловлен увеличением толщины реакционного слоя. Этот эффект связан с изменением соотношения вкладов реагентов на расстоянии максимального приближения и более удаленных частиц.

I. Введение. Постановка задачи.

Реакция электрохимического восстановления персульфат-иона S₂O₈^2- сыграла исключительную роль в развитии электрохимической кинетики, ярко высветив проблему электростатического взаимодействия реагент–электрод и положив начало тонким исследованиям большой группы процессов электровосстановления анионов. Основными экспериментально установленными особенностями восстановления S₂O₈^2- на ртути и ртутеподобных металлах являются [1-11]:

• наличие минимума тока на поляризационных кривых j(h) при отрицательных зарядах поверхности электрода в разбавленных растворах;
• увеличение тока в области минимума с ростом концентрации электролита фона;
• “катионный катализ”, т.е. существенное увеличение скорости разряда персульфат иона при изменении природы катионов фона в ряду Li⁺<Na⁺<K⁺<Rb⁺<Cs⁺;
• чрезвычайно слабая температурная зависимость, отвечающая нулевым (а в некоторых случаях небольшим отрицательным) энергиям активации.

,

(1)

где j – плотность тока, k_s - гетерогенная константа скорости; [С] – объемная концентрация реагента; n_i – заряд реагирующей частицы, - потенциал электрода. Соответственно, в координатах исправленной тафелевской зависимости (и.т.з.) () при корректном выборе величин в отсутствие специфической адсорбции теория предсказывает совпадение и.т.з. для металлов с различными потенциалами нулевого заряда и для разных концентраций фонового электролита. В случае персульфат-аниона такое совпадение в некотором приближении достигается при подстановке в качестве величины потенциала внешней плоскости Гельмгольца, но только для серий экспериментов с одним и тем же катионом фона.
Попытки учета в этой связи специфической адсорбции ионов цезия [13] показали, что существенное смещение и.т.з. при переходе от более сильно гидратированных катионов к катиону цезия в рамках теории замедленного разряда можно объяснить только в предположении о сильном локальном взаимодействии, т.е. о дискретной структуре двойного электрического слоя (ДЭС). Качественно это предположение согласуется с гипотезой о более высокой реакционной способности анион-катионных ассоциатов, образующихся в двойном слое, по сравнению с реакционной способностью свободных анионов. Следует, однако, отметить, что до недавнего времени при анализе кинетики восстановления анионов в водных растворах игнорировалась возможность параллельного участия в реакции ионных ассоциатов (например, ), образовавшихся в объеме раствора. Учитывая достаточно высокие константы ассоциации по первой ступени [14] и значительные концентрации фоновых катионов в исследуемых растворах, гипотезы [6,10] о природе “катионного катализа” требуют уточнения. Мы полагаем, однако, что этому должно предшествовать рассмотрение особенностей поляризационных кривых восстановления S₂O₈^2-, выходящее за рамки теории замедленного разряда, с целью установления истинных величин коэффициентов переноса и их зависимостей от потенциала (перенапряжения), а также факторов, определяющих такого рода зависимости.
В пользу изменения с потенциалом для подавляющего большинства растворов S₂O₈^2-(исключая Сs-содержащие) свидетельствуют широко известные серии и.т.з. [3]. Согласно [3], линеаризация и.т.з. достигается только при выборе локализации эффективного точечного реагента в плотной части двойного электрического слоя и, соответственно, при подстановке величин , превышающих по абсолютной величине потенциалы внешней плоскости Гельмгольца. С учетом реальной геометрии персульфат-аниона, оцениваемой из кристаллохимических данных [15], такая локализация крайне маловероятна, т.к. размер частицы заведомо превышает толщину плотной части двойного слоя. Недавние оценки “микроскопических” пси-прим эффектов показывают, что неравномерность зарядового распределения в частице персульфат-аниона не может быть причиной аномально высокой работы приближения при локализации в диффузной части двойного слоя [16]. Таким образом, нелинейность и.т.з. не удается объяснить выбором заниженных значений -потенциала.
С точки зрения современной теории переноса заряда в полярных средах, в широком интервале свободных энергий реакции аномалией следует считать именно постоянство , поскольку с ростом перенапряжения эта величина должна уменьшаться [17,18]. В случае восстановления гексацианоферрат-аниона (протекающего на ртути, как и обсуждаемая реакция, в области высоких перенапряжений), согласие наклонов поляризационных кривых и величин энергий активации с предсказаниями квантово-механической теории, полученными в рамках гармонического приближения, в целом вполне удовлетворительно [19] и свидетельствует о достижении при потенциалах –1.8 - -2.0 В (нас.к.э.) окрестности безактивационной области. К этому же выводу приводит как для гексацианоферрат-, так и для персульфат-анионов построение так называемых маркусовских и.т.з. [20]: при любых способах учета электростатических эффектов некоторые их участки имеют аномальный наклон, формально отвечающий отрицательным . Именно к такому результату должно приводить рассмотрение, игнорирующее перенос электронов с нефермиевских уровней, если перенапряжение достаточно велико, и теория Маркуса, соответственно, не применима.
Необходимо отметить важное качественное различие в тенденции изменения величины , оцениваемой из и.т.з. – если для гексацианоферрата эта величина плавно снижается с ростом перенапряжения, то для персульфата она, напротив, возрастает (в кажущемся противоречии с предсказаниями квантово-механической теории). Одним из обстоятельств, ответственным за такое аномальное поведение , может быть нарушение гармонического приближения из-за разрыва связи O-O при переносе электрона к персульфат-аниону. Иными словами, приближение линейного отклика при описании поверхности потенциальной энергии (ППЭ) вдоль внутримолекулярной координаты реакции (r) перестает работать, и, следовательно, “маркусовскую” внутрисферную энергию реорганизации уже нельзя использовать как параметр в расчетах энергии активации – истинная внутрисферная составляющая становится зависимой от других составляющих барьера. Строгое описание франк-кондовского барьера в таком случае [21] требует знания сечения ППЭ вдоль координаты r для реагента и продукта. Такое сечение может быть построено по результатам квантово-химических расчетов.
В настоящей работе моделирование реакции с разрывом связи впервые проведено для области высоких перенапряжений в окрестности безактивационного разряда, т.е. при расчете тока выполнено интегрирование по всему электронному спектру металлического электрода. При этом на молекулярном уровне учтены важнейшие электростатические и сольватационные эффекты, в том числе связанные с вкладом в токовый отклик частиц реагента, расположенных на разных расстояниях от поверхности. Предполагается, что именно перенос первого электрона с одновременным разрывом связи является лимитирующей стадией суммарного двухэлектронного процесса:

+ е --> +

(иногда в литературе для такой элементарной стадии употребляется термин “концертный механизм” [22,23]). Поэтому при расчете перенапряжения в качестве стандартного потенциала используется значение 1.45 В (н.в.э.) для редокс-системы /, [24]. Гипотеза о генерация сульфат-радикала при восстановлении персульфат–аниона на ртути находится в согласии с недавними данными [25].

II. Расчетные методы

Квантовохимические расчеты ионов , , и проводились ab initio методом Xартри–Фока-Рутана (SCF) [26, 27] , а также с использованием многочастичной теории возмущений Меллера-Плессе второго порядка (MP2) [27] и теории функционала плотности (DFT) с гибридным функционалом B3LYP [28] (табл.1). Два последних метода позволяют учесть эффект электронной корреляции, который особенно важен при описании разрыва химических связей. Системы с открытыми оболочками рассчитывались на основе неограниченной версии методов SCF и DFT. В таблице 1 представлены результаты расчетов длин связей и валентных углов персульфат–иона (см. их обозначения на рис. 1a) с использованием различных базисных наборов [26]. Наилучшее согласие с кристаллохимическими данными [15] достигается при использовании базиса 6-31G(d)(Количественного согласия величин расстояний и, в особенности, углов для моделируемого свободного аниона в полярной среде и аниона в кристаллической решетке K₂S₂O₈ ожидать, вообще говоря, трудно, но, как видно из таблицы, общие тенденции передаются правильно.) (согласие, разумеется, не является количественным, поскольку проводится расчет изолированной частицы). Влияние сольватации учитывалось в рамках континуальной теории реактивного поля (модель РСМ [29-31]).
Как видно из табл. 1, методы МР2 и DFT(B3LYP) приводят к практически одинаковым результатам. Поскольку метод MP2 более требователен к машинным ресурсам, все дальнейшие расчеты были проведены в рамках теории функционала плотности с базисом 6-31G(d). При изучении адсорбции с использованием кластерной модели металла 5d¹⁰6s²6p электроны атома Hg описывались дважды расщепленным базисным набором [32]. Эффект внутренних электронов учитывался посредством псевдопотенцала Хэя-Вадта [32]. Все квантовохимические расчеты проводились с использованием программных пакетов Gaussian-94, 98 [33, 34].

III. Структура реагента в объеме раствора

Геометрия полностью оптимизировалась для двух изомеров (cis- и trans-форм). Было обнаружено, что сольватация приводит к заметному изменению равновесной геометрии реагента. Согласно результатам расчета, trans-изомер персульфат-аниона является энергетически более устойчивым как в газовой фазе, так и в водном растворе (рис. 1б, кривые 1 и 2 соответственно). Зависимость полной энергии от угла вращения вокруг оси, проходящей через пероксидный фрагмент О-О, показывает, что переход из одной изомерной формы в другую носит безбарьерный характер (на рис. 1б нулевое значение угла отвечает cis-форме).

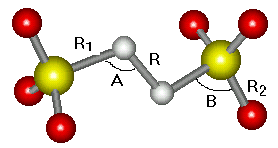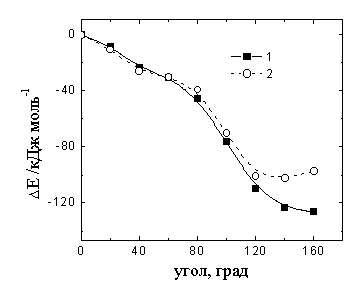Рис. 1. а - Равновесная структура trans-изомера по результатам квантовохимических расчетов методом функционала плотности с учетом сольватации (R= 0.718 нм , R1= 0.146 нм, R2= 0.147 нм, A= 109 град, B= 104 град); б - энергетический профиль, описывающий переход из cis- в trans-, построенный для газовой фазы (1) и с учетом сольватации (2).

Расчет зарядов на атомах, входящих в персульфатную частицу (табл. 2), проводили на основе малликеновского анализа заселенностей [26, 27], метода натуральных орбиталей (NPA) [35,36] и схемы ChelpG [36]. Использование последней схемы наиболее целесообразно, поскольку при этом заряды на атомах подбираются самосогласованно таким образом, чтобы индуцировать такой же потенциал, как и вся непрерывная зарядовая плотность реагента (продукта).
Эффективные сольватационные радиусы реагента и продукта (табл. 3) рассчитывали по методике [37]. Полученная величина r_eff cоставила для персульфат-аниона »0,35 нм, что близко к эффективному радиусу (0,31 нм) эллипсоида, описывающего частицу реагента (рис. 2а) .

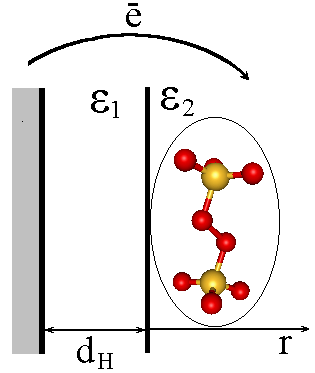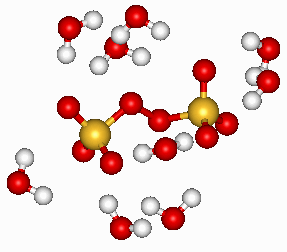Рис. 2. а - модель реакционного слоя для электрохимического восстановления персульфат-аниона; б - структура ближайшего сольватного окружения, рассчитанная в рамках “супермолекулярного” подхода для системы

IV. Адсорбционное взаимодействие реагента с ртутным электродом

Вопрос о специфическом взаимодействии реагента с электродом или, другими словами, о возможности проникновения частицы реагента в плотную часть ДЭС важен с точки зрения выбора реалистичной модели реакционного слоя и нуждается в специальном исследовании. Энергию адсорбции иона на электроде из раствора, , можно приближенно представить как сумму нескольких вкладов.
(1) Энергия адсорбции из газовой фазы, , для ориентации реагента, показанной на рис. 2а, рассчитывалась методом функционала плотности с привлечением кластерной модели для описания поверхности металла. Модельный двухслойный кластер состоял из 16 атомов ртути (10+6); ближайшее расстояние между атомами Hg принималось равным 0.3 нм. [38]. При проведении квантовохимических расчетов релаксация геометрии не учитывалась.
(2) Затраты энергии на потерю как минимум трех молекул воды из ближайшей сольватной оболочки реагента (частичная десольватация) при непосредственном контакте с металлом, . Как показали квантовохимические расчеты с использованием “супермолекулярных” моделей (см. рис.2б) средняя энергия связи одной молекулы воды с персульфат-ионом в ближайшей сольватной сфере составляет около 55 кДж/моль.
(3) Проигрыш в энергии, связанный с десорбцией нескольких молекул воды с поверхности ртутного электрода, . Согласно данным компьютерного моделирования методом молекулярной динамики [39], эффективная площадь, занимаемая одной молекулой H₂O в монослое на поверхности ртути, практически совпадает с площадью, приходящейся на один атом металла. Поэтому предполагалось, что число вытесняемых молекул воды можно приближенно оценить из отношения ()² , где 0.15 нм соответствует половине ближайшего расстояния между атомами ртути. При расчете величины также использовались результаты, приведенные в работе [40].
Отметим, что во всех расчетах подразумевалась незаряженная поверхность ртутного электрода. Как следует из результатов, представленных в Таблице 3, адсорбция персульфат-иона из газовой фазы характеризуется значительным тепловым эффектом; при этом частичный перенос заряда на металл составляет около 0.5е (в рамках анализа заселенностей по Малликену). В то же время, благодаря вкладам (2) и (3), результирующее значение для персульфат-иона становится положительным (см. Табл.3). Таким образом, проведенные оценки не предсказывают специфической адсорбции на ртутном электроде, по крайней мере при отрицательных и нулевом зарядах поверхности. Это заключение позволяет ограничиться моделью реакционного слоя, представленной на рис.2а, и не рассматривать возможность частичного проникновения реагента в плотную часть ДЭС.

V. Теоретическое описание

Согласно современной теории неадиабатических процессов переноса заряда на межфазной границе металл/раствор [18], выражение для плотности тока можно записать следующим образом:

,

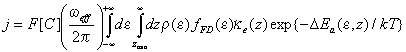(2)

где DE_a - энергия активации; k_e - электронный трансмиссионный коэффициент; w_eff - эффективная частота колебаний поляризации растворителя (10¹³ с^-1); z - расстояние от центра реагента до поверхности электрода (z_min – соответственно, кратчайшее расстояние); e - энергетический уровень электрона в металле; r(e) - плотность электронных состояний электрода, - функция Ферми – Дирака (e_F – уровень Ферми). Во всех последующих расчетах тока величина объемной концентрации персульфат-иона [С] принималась равной 0.5 мМ, как в классических экспериментах [3] и многих других.
Ключевыми параметрами уравнения (2) являются энергия активации DЕ_а и электронный трансмиссионный коэффициент k_e.
Согласно подходу, развитому в [21] для случая произвольной формы сечения ППЭ вдоль одной эффективной координаты внутримолекулярной реорганизации (r), расчет энергии активации сводится к решению системы уравнений:

,

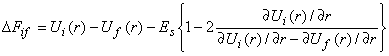(3)

,

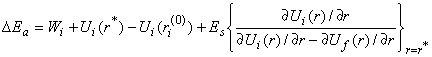(4)

где - одномерные потенциалы, описывающие ППЭ как функцию от для начального (i) и конечного (f) состояний; отвечает минимуму терма ; - корень уравнения (3); E_s – энергия реорганизации растворителя, W_i – работа подвода реагента.

Выражение для теплового эффекта имеет вид:

,

(5)

где -работа приближения(отвода) реагента (продукта) реакции; - перенапряжение.
Величина энергии реорганизации растворителя оценивалась по формуле

,

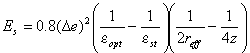(6)

Согласно оценкам для других эллиптических реагентов близкого размера и формы [41], более точный расчет по модели проводящих эллипсоидов вращения не приводит к существенным отличиям Е_s. Коэффициент 0.8 в правой части уравнения (6) приближенно учитывает некоторое уменьшение франк-кондоновского барьера, обусловленное квантовыми модами растворителя [42].
Работы сближения рассчитывались следующим образом:

,

(7)

где - распределение зарядов в частицах реагента (продукта); - потенциал в объеме полости, описывающей частицу.
Выражение (7) основано на идее учета детального зарядового распределения в молекулах при расчете двойнослойных поправок (“микроскопический” - эффект [16]). В настоящей работе использовалась модель, учитывающая изменение поля двойного слоя внутри эффективной сферы, описывающей реагент, вследствие заметного отличия диэлектрической проницаемости внутри такой полости от объемного значения в растворе (см. более детальное изложение в [16]). Для описания поля диффузной части ДЭС использовались Гуи-Чапменовские соотношения.
Отметим, что при построении модельных поляризационных кривых, описывающих восстановление , наиболее важен учет работ приближения реагентов (). Тестовые расчеты показали, что в наиболее интересной области больших перенапряжений работы удаления продуктов незначительно влияют на величину теплового эффекта.
Электронный трансмиссионный коэффициент () в общем может быть рассчитан на основе подхода Ландау-Зинера [43]:

,

(8)

В свою очередь, выражение для записывается следующим образом [40]:

.

Ключевую роль в оценке параметра играет - половина резонансного расщепления реакционных термов в точке переходного состояния. В данной работе для расчета величины использовалась теория возмущений, в рамках которой имеем:

,

(9)

где оператор - возмущение, приводящее к переносу электрона; волновая функция металла; акцепторная молекулярная орбиталь.
В общем случае выражение для принимает вид:

,

(10)

где - кулоновский потенциал, наводимый зарядовым распределением реагента; - потенциал ДЭС; - заряд электрона. В рассматриваемом случае, когда реагент не проникает в плотную часть ДЭС, второй член в уравнении (10) не играет значительной роли. В дальнейших расчетах предполагалось, что .
Величина рассчитывалась следующим образом:

,

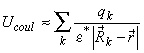(11)

где - атомные заряды; - положения ядер в молекуле реагента; - диэлектрическая проницаемость межфазной границы, зависящая в общем случае от . В наших расчетах использовалась специально подобранная функция , имитирующая переход от значения в объеме растворителя (78) к более низкому значению в плотной части ДЭС (5).
Для процесса переноса электрона, протекающего с разрывом химических связей, коэффициент в уравнении (8) записывается в виде [21]:

,

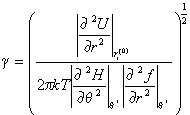(12)

где , и .
Волновую функцию электронов в металле рассчитывали приближенно, исходя из профиля электронной плотности n(z), определенной как

.

(13)

Плотность n(z) можно описать с использованием функций Смита [44-46]:

.

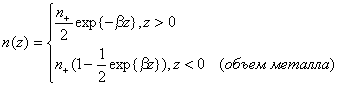(14)

где n₊ - плотность ядерного остова ртути ( = 86.46 нм^-3 [46]).
Важно подчеркнуть отличие используемого подхода от развитого недавно авторами [44, 45]. В данных работах при вычислении плотности тока вводилась электронная плотность металлического электрода, зависящая не только от расстояния, но и от плотности энергии электронных состояний. При этом в результирующем выражении для плотности тока возникает отношение двух характерных энергетических параметров электронного спектра металла [44, 45]. В настоящей работе плотность электронных состояний вычислялась независимо (см. ниже).
Важным параметром в системе (14) является , величина которого определяет характерный масштаб затухания . Для ртути расчеты методом функционала плотности с использованием модели “желе” приводят к значению , равному 22.97 нм^-1 [46]. Независимые расчеты профиля электронной плотности n(z) вблизи уровня Ферми, проведенные для 5 слоев кристаллической ртути методом линеаризованных присоединенных плоских волн (ЛППВ) [47] в приближении “muffin-tin” [48], позволили сделать два важных вывода. Во-первых, численные значения n(z) в области z > 0, усредненные вдоль плоскости металла, хорошо аппроксимируются одной экспонентой (см. уравнение (14), при z>0). Во-вторых, значение , предсказанное методом ЛППВ (21.17 нм^-1) близко к результату, полученному на основе модели “желе”.
Отметим, что в общем случае зависит от плотности заряда электрода, что в свою очередь должно привести к зависимости электронного трансмиссионного коэффициента от перенапряжения. Данное обстоятельство может оказаться существенным в области безактивационного разряда, индуцируя дополнительный рост тока. Однако, поскольку корректный учет такого эффекта приводит к существенному усложнению модели, то зависимость от заряда электрода в настоящей работе не учитывалась.
Плотность состояний, фигурирующая в уравнении для плотности тока (1), рассчитывалась в рамках модели свободного электронного газа [49]:

, .

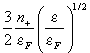(15)

где и .
Расчет уровня Ферми для ртути, с использованием данной модели при =86.46нм^-3 (см. уравнение (14)) приводит к значению =7.12 эВ, что находится в неплохом согласии с экспериментальными данными (6.8 эВ [50]). Плотность состояний на уровне Ферми , вычисленная таким образом, хорошо согласуется с результатами расчетов методом ЛППВ.
Модельные зависимости плотности тока от перенапряжения рассчитывались по точкам с шагом по перенапряжению 0.05 – 0.1 В, достаточным для адекватного представления формы поляризационных кривых.

VI. Обсуждение результатов

Как следует из данных по гомогенным редокс-реакциям [24] и из квантово-химических расчетов, перенос первого электрона на приводит к разрыву “пероксидной” связи О-О с образованием радикала и сульфат-иона . Поэтому при построении одномерных ППЭ для начального и конечного состояний именно связь О-О была выбрана в качестве эффективной координаты внутрисферной реорганизации. При этом расстояние между атомами О-О менялось с некоторым шагом, а остальные длины связей и валентные углы полностью оптимизировались. В расчетах ППЭ учитывались эффекты сольватации в рамках модели PCM. Следует, однако, подчеркнуть, что в исследуемом диапазоне изменения межатомного расстояния O-O влияние растворителя на форму ППЭ не привело к появлению заметных отличий от хода термов, построенных для газовой фазы. Как видно из рисунка 3, ППЭ для начального состояния хорошо описывается потенциалом Морзе (кривая 1 рис. 3):

.

(16)

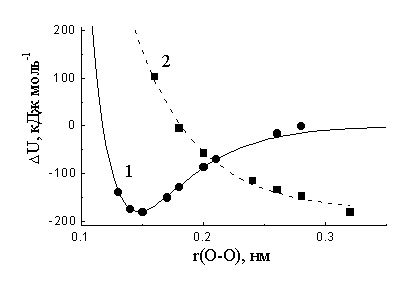Рис.3. Полная энергия персульфат-аниона в окисленном (1) и восстановленном (2) состоянии как функция от внутрисферной координаты реакции r(O-O); пунктиром показана экспоненциальная аппроксимация, сплошной линией - аппроксимация потенциалом Морзе.

Как показали оценки, частота колебания связи О-О в окрестности минимума (345 см^-1) близка к классической области. Для “распадного” терма (кривая 2 рис. 3) наиболее удачной является аппроксимация экспонентой:

.

(17)

Для параметров, входящих в выражения (16) - (17) получены следующие значения: =23.8 нм^-1; D= 180 кДж/моль; = 0.147 нм и =26 нм^-1; B=598 кДж/моль.
Реакции с разрывом связи в органической электрохимии традиционно описываются полуфеноменологической моделью Савьяна [22, 23], параметр которой D имеет смысл энергии разрыва связи. Расчеты поляризационных кривых в рамках [22, 23] для так называемого “концертного механизма” (т.е. разрыва связи непосредственно в элементарном акте) предсказывают, что наилучшее согласие расчета и эксперимента по величинам тока в минимуме достигается при D = 420 кДж/моль. Однако эта величина существенно отличается от энергии разрыва пероксидной связи (180 кДж/моль), полученной из квантовохимических расчетов. Причиной разногласия является неприменимость теории Савьяна для произвольной формы ППЭ. В то же время модель [22, 23] представляет собой частный случай системы уравнений (3)-(4) при . В рассматриваемом случае это условие, очевидно, нарушено.
Aнализ акцепторной орбитали реагента (высшая занятая молекулярная орбиталь, рассчитанная для иона при =0.147 нм) показал, что она имеет существенно делокализованный характер (рис. 4а). Следует отметить, что наибольший вклад в нее вносят 2s- и 2p- орбитали атомов кислорода пероксидной группы, а вклад 3d- орбиталей атомов серы весьма незначителен. Кроме того, было обнаружено, что учет влияния растворителя в рамках модели РСМ слабо влияет на структуру акцепторной орбитали (в дальнейших расчетах трансмиссионного коэффициента этим эффектом пренебрегали).

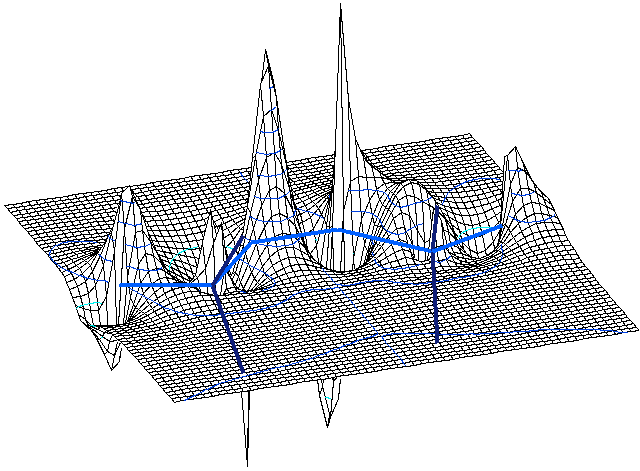Рис.4. а - Трехмерное сечение акцепторной орбитали персульфат-иона: б – исследуемые ориентации; в - зависимость электронного трансмиссионного коэффициента от расстояния – электрод, рассчитанная для двух ориентаций реагента.

Электронный трансмиссионный коэффициент как функцию от z рассчитывали для двух ориентаций реагента (рис. 4б). Полученные зависимости представлены на рис.4в. В исследованном интервале z спад с расстоянием не удается удовлетворительно описать единой экспоненциальной зависимостью, грубая аппроксимация соответствует снижению на порядок экспоненты на расстоянии 0.085 нм. Ниже некоторые расчеты величин lg проводились для двух возможных значений толщины плотной части ДЭС (=0.4 и 0.6 нм), с целью избежать неопределенности, обусловленной отсутствием точных сведений о строении межфазной границы. Как видно из рисунка 4в, перенос электрона носит неадиабатический характер. Отметим также, что более предпочтителен перенос электрона к реагенту в ‘горизонтальной’ ориентации.
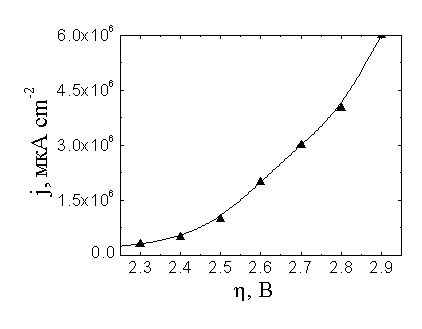
С целью предварительной характеристики процесса в исследуемой области перенапряжений была построена модельная поляризационная кривая для гипотетической ситуации = 0, т.е. при отсутствии электростатических взаимодействий реагента и продукта с полем ДЭС (рис.5)

Рис. 5. Модельная поляризационная кривая восстановления , рассчитанная при нулевых энергиях сближения для реагентов и продуктов (=0).

В этом случае основной вклад в энергию активации вносят внутримолекулярная энергия реорганизации и перенапряжение. Как показали расчеты с использованием выражения (2), значимый вклад в величину тока вносят энергетические уровни в металле, лежащие на 0,2 – 0,3 эВ глубже уровня Ферми. Этот эффективный энергетический интервал оценен по теореме о среднем интегральном:

,

(18)

где .
Аналогичные оценки на основе расчетов [19] для гексацианоферрат-аниона приводят к близким величинам уже в области меньших перенапряжений, что вполне объяснимо с учетом более низкого внешнесферного вклада в барьер для реакции без разрыва связи.
Из рис.5 видно, что в исследованном интервале 2.3– 2.9 В наблюдается достаточно медленный рост тока, что характерно для окрестности безактивационной области. Как подтверждение близкого к безактивационному характера разряда можно рассматривать чрезвычайно низкие значения энергии активации, оцениваемые из опытных температурных зависимостей [6]. Этот факт, однако, может иметь и другие объяснения, связанные с изменением конфигурации реакционного слоя с температурой.
Истинный коэффициент переноса в исследованной области перенапряжений изменяется от 0.06 до 0.02. При столь низких его значениях наблюдаемый минимум тока на экспериментальных поляризационных кривых не может быть объяснен в рамках традиционного рассмотрения только двух факторов (усиливающегося с ростом отрицательного заряда отталкивания реагента и увеличения скорости процесса с ростом перенапряжения). 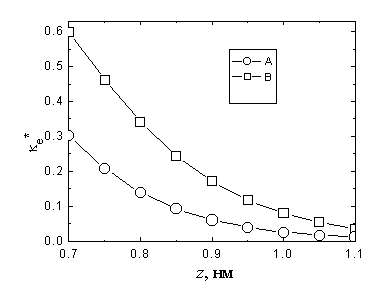Поэтому в дальнейшем специальное внимание уделено учету зависимости от расстояния как фактору, независимо обеспечивающему рост тока восстановления анионов при высоких отрицательных зарядах поверхности [51]. Роль этого фактора подробно исследовалась для двух ориентаций реагента, показанных на рис. 4б. Работы сближения W_i, описывающие взаимодействие с диффузной частью ДЭС, приведены на рис. 6. Как видно из рисунка 6, “ориентационная” зависимость для персульфат-иона выражена слабо, поэтому в дальнейших расчетах ограничились случаем, когда ось, соединяющая атомы серы в персульфат-ионе параллельна поверхности электрода (ориентация В), основываясь на более высоких значениях трансмиссионного коэффициента для такой ориентации.

Рис.6. Работа сближения аниона S2O82-, рассчитанная в зависимости от расстояния центра эффективной сферы до внешней плоскости Гельмгольца (z); рассматривались ориентации А и В (см. рис.4б).

Используя теорему о среднем интегральном, выражение для тока (3) удобно представить в виде:

,

(19)

где - расстояние от электрода, при котором произведение принимает максимальное значение; традиционно называется реакционным объемом или толщиной реакционного слоя.
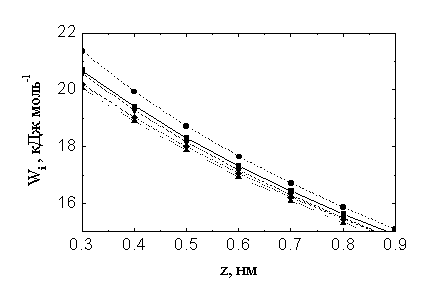
Результаты вычислений показали, что для исследуемого случая (см. выражение (3)). Это согласуется с оценками [51]: для обсуждаемых концентраций электролита фона характеристический параметр [51] составляет не менее 10, т.е. остается существенно выше критического значения, при котором ожидается смещение основной зоны реакции от плоскости максимального приближения (Характеристический параметр [51] представляет собой отношение наклона зависимости ln от z к обратной дебаевской длине.). В таблице 3 приведены значения , рассчитанные по формуле (19) при концентрации фона 0.01М. Как видно, реакционный объем существенно зависит от перенапряжения (заряда электрода). В то же время моделирование демонстрирует крайне слабую зависимость от концентрации фонового электролита в исследованном (сравнительно узком) интервале. Для рассмотренного выше упрощенного сценария = 0 (рис.5) величина не превышала 0.05 нм и оказывалась, как и следовало ожидать, практически постоянной в области перенапряжений 2.9 - 3.6 В. Таким образом, за ее рост в расчетах, учитывающих электростатические взаимодействия, ответственно именно существование распределения потенциала в диффузной части ДЭС.
Тестовые расчеты для модельных точечных регентов, выполненные по аналогии с расчетами [51] и с использованием представленной выше зависимости трансмиссионного коэффициента от расстояния, предсказывают существенное увеличение с концентрацией электролита фона только в области > 1M. Соответственно, в растворах с концентрацией до 0,1 М эффект изменения в серии опытов с разными добавками индифферентного электролита можно прогнозировать только при очень слабой зависимости трансмиссионного коэффициента от расстояния (характеристический параметр 0,3 и более нм). Это в принципе возможно при очень слабом электронном перекрывании электрод/реагент.
Поскольку для обсуждаемых составов раствора зависимость от концентрации фона не проявляется, учет этого параметра не должен существенно влиять на выполнение классического критерия, используемого при построении и.т.з. – совпадение кривых для разных концентраций. В то же время зависимость от перенапряжения, усиливающаяся с ростом по абсолютной величине заряда электрода, существенна для интерпретации наклонов и.т.з. В частности, увеличение коэффициента переноса с ростом перенапряжения вполне объяснимо ростом , но не является специфическим следствием разрыва связи.
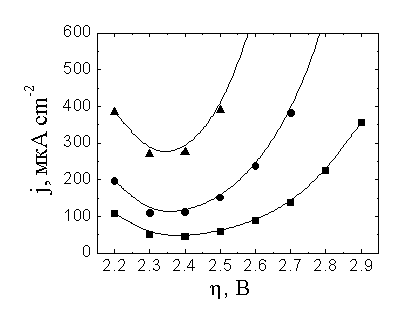
На рис. 7а,б представлены модельные поляризационные кривые, учитывающие как рост , так и вклады нефермиевских уровней. Последние не изменяют формы кривых, но приводят к увеличению рассчитанных значений тока. Учитывая некоторую неопределенность модели межфазной границы, моделирование проводили для двух значений толщины плотной части ДЭС (х_Н). Более высокие токи при использовании меньшего х_Н=0.4 нм получаются в расчете из-за того, что этой модельной величине соответствуют меньшие z_min и, следовательно, большие .

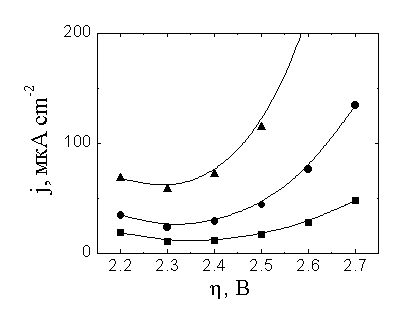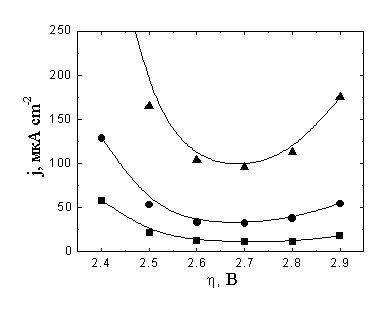Рис.7. Модельные (а, б) и экспериментальные [5] (в) поляризационные кривые восстановления аниона S2O82- на ртутном электроде при различных концентрациях фонового электролита NaF (0.02М, 0.01М и 0.005М); концентрация реагента равна 0.5 мM.

Для сравнения на рис. 7в представлены характерные экспериментальные кривые восстановления персульфат-аниона в растворах с теми же концентрациями 1,1-валентного фонового электролита. Модельные кривые рис. 7а,б в целом удовлетворительно описывают общие тенденции для этой серии кривых и находятся с ними в полуколичественном согласии. Однако очевидно, что учет природы катиона требует как минимум аналогичного моделирования процессов восстановления ионных пар.
Минимум тока на модельных кривых слегка смещен по сравнению с экспериментальным в сторону менее отрицательных потенциалов. Положение минимума довольно чувствительно к конкретной зависимости от потенциала (заряда), поэтому не исключено, что при замене Гуи-Чапменовской модели диффузного слоя на более совершенную в будущем этот участок удастся смоделировать более достоверно.
Уточнение расчетов возможно в принципе на основе более реалистичных моделей электронного перекрывания: параметр весьма чувствителен к описанию электронной плотности металлического электрода. Подчеркнем, что для описания наиболее важного качественного эффекта роста тока в области высоких перенапряжений для обсуждаемой реакции нет необходимости дополнительно моделировать рост с увеличением отрицательного заряда электрода. Ранее необходимость учета этого обстоятельства обсуждалась в [19] в связи с не нашедшим объяснения ростом тока восстановления гексацианоферрат-аниона в безактивационной области. На основе результатов этой работы возможно альтернативное объяснение проблемы, затронутой в [19].

Заключение

В настоящее время фундаментальная электрохимическая кинетика находится в стадии перехода от феноменологического описания поляризационных кривых к анализу физических закономерностей элементарного акта. На этом этапе классические модельные реакции восстановления анионов могут сыграть совершенно новую роль в экспериментальной проверке важнейших положений теории. В числе таких реакций достойное место займет, по-видимому, и электровосстановление персульфат-аниона, исследования которого продолжаются на гранях монокристаллов [52-55], в том числе и на переходных металлах. Обсуждаемая реакция востребована в современных исследованиях по построению новых моделей двойного слоя [56].
Первая попытка теоретической интерпретации данных [1] была предпринята В.Г.Левичем на основе представлений о неравновесном двойном электрическом слое [57]. Соответствующее математическое описание для реальных систем, одновременно содержащих несколько видов ионов разной зарядности, оказывается достаточно сложным [58], и исчерпывающий анализ справедливости гипотезы Левича до сих пор не выполнен. Полученные в настоящей работе результаты позволяют, однако, достичь самосогласованной интерпретации сложной формы поляризационных кривых, зависящей от концентрации электролита фона, оставаясь в рамках представлений о равновесном двойном слое. При этом описанный выше эффект увеличения толщины реакционного слоя следует непосредственно рассматривать как пси-прим-эффект, количественный анализ которого выполнен с учетом реального строения реагента.
Необходимо отметить, что в условиях притягательного взаимодействия реагента с полем ДЭС увеличение заряда электрода по абсолютной величине должно приводить к противоположному эффекту – сужению реакционного слоя. Такое сужение будет, однако, значительно мене выраженным, поскольку, как показывают оценки, вклад процесса с участием реагента на расстоянии максимального приближения при реальных параметрах систем всегда останется преобладающим. Именно по этой причине не утрачивает силы приведенный А.Н.Фрумкиным в [59] анализ данных по разряду иона гидроксония. Согласно [59], в этом случае удаленные от поверхности реагенты фактически не вносят вклада в измеряемый ток.
Авторы благодарны Д. Хмелевскому (Воронежский государственный университет) за помощь в проведении расчетов методом ЛППВ. Работа поддержана РФФИ (проект №. 99-03-32367).

Литература

1. Крюкова Т.А.//ДАН СССР. 1949. Т.65. С.517.
2. Фрумкин А.Н., Флорианович Г.М.// Доклады АН СССР. 1951. Т.80. С.907.
3. Фрумкин А.Н., Петрий О.А.//Доклады АН СССР. 1962. Т. 147. С.418.
4. Петрий О.А., Фрумкин А.Н.// Доклады АН СССР. 1962. Т.146. С. 1121.
5. Frumkin A.N., Petrii O.A., Nikolaeva-Fedorovich N.V.// Electrochim. Acta. 1963. V.8. P.177.
6. Gierst L., in Trans. Symp. Electrode Processes, Philadelphia, 1959. N.-Y., Wiley, 1961, p.109.
7. Николаева-Федорович Н.В., Петрий О.А., Дамаскин Б.Б., Фуражкова Г.А.// Вестник МГУ, Сер. 2 Химия. 1961. Т.17. С.40.
8. Giacomelli A., Indelli A.// Trans. Faraday Soc. 1968. V.65. P.2160.
9. Fawcett W.R., Levie S.//J.Electroanal. Chem. 1973. V.43. P.301.
10. Frumkin A.N., Nikolaeva-Fedorovich N.V., Beresina N.P., Keis Kh.E.//J.Electroanal. Chem. 1975. V.58. P.189.
11. Fawcett W.R.//J.Electroanal. Chem. 1969. V.22. P.19.
12. Фрумкин А.Н. Электродные процессы. Избранные труды. М: Наука, 1987. 334 с.
13. Дамаскин Б.Б., Федорович Н.В.//Электрохимия. 1975. Т.11. С. 999.
14. Ananthaswamy J., Sethuram B., Navaneeth T.// Indian J. Chem. 1977. V.15A. P.177.
15. Наумов Д.Ю., Вировец А.В., Подберезская Н.В., Новиков П.Б. // Ж.структ. химии. 1977. Т.38. С. 772.
16. Цирлина Г.А., Петрий О.А., Глухов Д.В., Назмутдинов Р.Р.//Электрохимия. 2002. Т.38. N 1.
17. Marcus R.A. //J. Chem. Phys. 1956. V.24. P.966.
18. Kuznetsov A.M. Charge Transfer in Physics, Chemistry and Biology. Mechanisms of Elementary Processes and Introduction to the Theory, Gordon and Breach Science Publishers, Berkshire, 1995.
19. Титова Н.В., Цирлина Г.А., Назмутдинов Р.Р., Петрий О.А.//Электрохимия. 2001. Т.37. С.21.
20. Г.А.Цирлина, О.А.Петрий, А.М.Кузнецов, Ю.И.Харкац//Электрохимия. 1999. Т.35. С.938.
21. Kuznetsov A.M., German E.D.// J.Phys. Chem. 1994.
22. Saveant J.-M.//J. Amer. Chem. Soc. 1987. V.109. P.6788.
23. Saveant J.-M.// J. Amer. Chem. Soc. 1992. V.114. P.10595.
24. Stanbury D.M., in Adv. Inorg. Chem. (Ed. A.G.Sykes). 1989. V.33. P.69.
25. Song J., Fu H., Guo W.// J.Elctroanal. Chem. 2001. V.511. P.31.
26. Hehre W.J., Radom L., Schleyer P.v.R., Pople J.A. Ab initio Molecular Orbital Theory. J. Wiley & Sons, NY, 1986.
27. Levine I.N. Quantum Chemistry. Prentice Hall, Inc., New Jersey, 1991.
28. Kohn W., Becke A.D., Parr R.G. //J. Phys. Chem. 1996. V.100. P.12974.
29. Tomassi J., Persico M. //Chem. Rev. 1994. V.94. P.2027.
30. Cances E., Mennuchi B., Tomassi J. //J. Chem. Phys. 1997. V.107. P.3032
31. Barone V., Cossi M. //J. Phys. Chem. 1998. V. A102. P.1995.
32. Hay P.J., Wadt W.R. //J. Chem. Phys. 1985. V.82. P.270.
33. Gaussian 94, Revision D.1, M.J. Frisch, G.W. Trucks, H.B. Schlegel et al., Gaussian, Inc.:Pittsburgh PA, 1995.
34. Gaussian 98, Revision A.3, M.J. Frisch, G.W. Trucks, H.B. Schlegel et al., Gaussian, Inc., Pittsburgh PA, 1998.
35. Reed A.E., Curtiss L.A., Weinhold F. //Chem. Rev. 1988. V.88. P.899.
36. Breneman C.M., Wiberg K.B. //J. Comp. Chem. 1990. V.11. P.361.
37. Nazmutdinov R.R., Tsirlina G.A., Kharkats Yu.I., Petrii O.A., Kuznetsov A.M.//Electrochim. Acta. 2000. V.45. P.3521
38. Nazmutdinov R.R., Probst M., Heinzinger K. //J. Electroanal. Chem. 1994. V.369. P.227.
39. Bocker J., Nazmutdinov R.R., Spohr E., Heinzinger K. //Surf. Sci. 1995. V.335. P.372.
40. Назмутдинов Р.Р. Электрохимия. 2002ю Т.38. №1.
41. Nazmutdinov R.R., Tsirlina G.A., Kharkats Yu.I., Petrii O.A., Probst M.// J.Phys. Chem. 1998. V.102. P.686.
42. Герман Э.Д., Кузнецов А.М.//Электрохимия. 1990. Т.26. С.931.
43. Кришталик Л.И. Электродные реакции. Механизм элементарного акта. М.: Наука, 1979. С. 109.
44. Kornyshev A.A., Kuznetsov A.M., Ulstrup J. //J. Phys. Chem. 1994. V.98. P.3832.
45. Kornyshev A.A., Kuznetsov A.M., Nielsen J.U., Ulstrup J. //Phys. Chem. Chem. Phys. 2000. V.2. P.141.
46. Dzhavakhidze P.G., Kornyshev A.A., Tsitsuashvili G.I. //Solid State Commun. 1984. V.52. P.401.
47. Krakauer H., Posternak M., Freeman A.J. //Phys. Rev. V. B19. P.1706.
48. Немошкаленко В.В., Кучеренко Ю.Н. Методы вычислительной физики в теории твердого тела. Электронные состояния в неидеальных кристаллах. Киев: Наукова думка, 1986. 296с.
49. Ашкрофт Н., Мермин Н. Физика твердого тела. Т.1. М: Мир, 1979. 400с.
50. Ballentine L., Chan T. Liquid metals. Tokio, 1972.
51. Gavaghan D.J., Feldberg S.W.//J.Electroanal. Chem.. 2000. V.491. P.103
52. Levi M.D., Fedorovich N.V., Damaskin B.B.//Can.J.Chem. 1981. V.59. P.2019.
53. Thomberg T., Lust E.//J.Electroanal. Chem. 2000. V.485. P.89.
54. Samec Z., Doblhofer K.//J.Electroanal. Chem. 1997. V.432. P.205.
55. Samec Z., Bittner A.M., Doblhofer K.// J.lectroanal. Chem. 2001. V.499. P.129.
56. Дамаскин Б.Б., Стенина Е.В., Батурина О.А., Свиридова Л.Н. //Электрохимия. 1998. Т.34. С.1083.
57. Левич В.Г.// Доклады АН СССР. 1949. Т.67. С. 309.
58. Воротынцев М.А., в сб. “Итоги науки и техники. Сер. Электрохимия”. М.: ВИНИТИ, 1979, т.14, с.57.
59. Frumkin A.// Z. phys. Chem. 1933. Bd.164. S.121.

Таблица 1. Значения длин связей и валентных углов персульфат-иона (trans-изомер), рассчитанный различными квантово-химическими методами с использованием трех базисных наборов.

	Расчет									Эксперим
		SCF			MP2			DFT (B3LYP)		По данным [15]
	4-31g	6-31g	6-31g(d)	4-31g	6-31g	6-31g(d)	4-31g	6-31g	6-31g(d)
R/ нм	0.1793	0.1799	0.1678	0.2038	0.2024	0.1753	0.1992	0.1976	0.1754	0.1494
R1/ нм	0.1575	0.1618	0.1439	0.1594	0.1621	0.1476	0.1608	0.1637	0.1479	0.1646
R2/ нм	0.1442	0.1446	0.1404	0.1541	0.1542	0.1491	0.1484	0.1483	0.1478	0.1422
A/ гр	103.93	104.22	103.54	103.33	103.79	103.07	103.56	103.95	103.30	106.15
B/ гр	132.37	132.49	131.41	128.69	129.51	129.02	130.60	131.57	130.19	105.41

Таблица 2. Атомные заряды в ионе , рассчитанные в рамках трех различных схем анализа заселенностей.

атом	ChelpG	NPA	Mulliken
S	1.06	2.55	1.19
Operox	-0.29	-0.53	-0.38
O	-0.60	-1.01	-0.61

Таблица 3. Равновесное расстояние от центра реагента до поверхности ртутного электрода (z_min ), эффективный радиус сферы, описывающей ион (r_eff ), составляющие энергии адсорбции иона и ее результирующие значение иона (кДж моль^-1), рассчитанные для персульфат-иона.

	zmin / нм	reff / нм
	0.38	0.36	-231	+135	+115	+19

Таблица 4. Реакционный объем (нм) в зависимости от перенапряжения , рассчитанный для электрохимического восстановления при двух различных значениях толщины плотной части ДЭС ().

/ В	2.1	2.2	2.3	2.4	2.5	2.6	2.7	2.8	2.9
= 0.4 нм	0.129	0.142	0.158	0.177	0.195	0.204	0.235	0.255	0.280
= 0.6 нм	0.131	0.143	0.155	0.168	0.178	0.188	0.198	0.206	0.216

Вернуться