![]() Резонансное туннелирование, фундаментальное квантово-механическое явление
прохода электроном с единичной амплитудой границ классически недоступных
областей в сложных молекулах, агрегатах, кластерах, твердых телах, которое
впервые наблюдали в квантовых ямах четверть века назад вольт-метрическими
[1] и, позднее, оптическими [2,3] методами. Этот пограничный волновой эффект
лег в основу работы субмикронных диодов и триодов, однобитных переключателей,
модуляторов и генераторов света [4] и породил новые направления мезоскопических
исследований [5]. Особые возможности для изучения туннельных резонансов
в молекулярных системах предоставляет конфигурация СТМ (квазиодномерный
зонд — диэлектрический зазор — проводящая поверхность), позволяя сканировать
промежуточные электронные уровни и, следовательно, создавать резонансные
условия для «двойного туннелирования» [6]. Предложенная в [7] методика
изготовления зондов для двойного туннелирования (последовательное осаждение
ультратонкой полимерной пленки и проводящего кластера на острие обычного
Pt-Ir-зонда) имеет ряд ограничений: затруднено однозначное определение
характерных размеров отдельных элементов формирующегося покрытия, а минимально
достижимые толщины пленки и диаметры кластеров оказываются не менее 2–3
нм. Альтернативным вариантом может быть осаждение на острие зонда «готовых»
наноструктур [8], например, молекулярных кластеров, включающих локализованные
окислительно-восстановительные центры.
Резонансное туннелирование, фундаментальное квантово-механическое явление
прохода электроном с единичной амплитудой границ классически недоступных
областей в сложных молекулах, агрегатах, кластерах, твердых телах, которое
впервые наблюдали в квантовых ямах четверть века назад вольт-метрическими
[1] и, позднее, оптическими [2,3] методами. Этот пограничный волновой эффект
лег в основу работы субмикронных диодов и триодов, однобитных переключателей,
модуляторов и генераторов света [4] и породил новые направления мезоскопических
исследований [5]. Особые возможности для изучения туннельных резонансов
в молекулярных системах предоставляет конфигурация СТМ (квазиодномерный
зонд — диэлектрический зазор — проводящая поверхность), позволяя сканировать
промежуточные электронные уровни и, следовательно, создавать резонансные
условия для «двойного туннелирования» [6]. Предложенная в [7] методика
изготовления зондов для двойного туннелирования (последовательное осаждение
ультратонкой полимерной пленки и проводящего кластера на острие обычного
Pt-Ir-зонда) имеет ряд ограничений: затруднено однозначное определение
характерных размеров отдельных элементов формирующегося покрытия, а минимально
достижимые толщины пленки и диаметры кластеров оказываются не менее 2–3
нм. Альтернативным вариантом может быть осаждение на острие зонда «готовых»
наноструктур [8], например, молекулярных кластеров, включающих локализованные
окислительно-восстановительные центры.
![]() В настоящей работе экспериментально изучается резонансное туннелирование
через такие центры и проводится компьютерное моделирование рассеяния электрона
в простейшей модели металл — молекула — металл.
В настоящей работе экспериментально изучается резонансное туннелирование
через такие центры и проводится компьютерное моделирование рассеяния электрона
в простейшей модели металл — молекула — металл.
![]() Для иллюстрации возможности резонансного туннелирования в молекулярных
системах были использованы гетерополисоединения (ГПС) М4[PtMo6O24] (М =
К или Na) со структурой Андерсона [9]. Нанесение кластеров осуществлялось
путем выдержки острия зонда из сплава Pt c 10–20 ат.% Ir (механическая
заточка) в насыщенных водных растворах ГПС на воздухе при разомкнутой цепи
в течение 10–12 ч. Туннельные спектры систем «модифицированный зонд — Рt-фольга»
регистрировали на воздухе, используя установку LitScan2 [10]. Базовые значения
туннельного тока составляли 0,2–1 нА, туннельного напряжения — 100–200
мВ, характерные времена квадратных импульсов напряжения — 250 мкс, длительность
интервалов между импульсами — 200 мс. Методические аспекты выбора режимов
измерений, обеспечивающих неизменность положения зонда, подробно рассмотрены
в [10]. В контрольных опытах использовали обычные зонды и Pt-фольгу, модифицированную
при помощи ГПС по аналогичной методике.
Для иллюстрации возможности резонансного туннелирования в молекулярных
системах были использованы гетерополисоединения (ГПС) М4[PtMo6O24] (М =
К или Na) со структурой Андерсона [9]. Нанесение кластеров осуществлялось
путем выдержки острия зонда из сплава Pt c 10–20 ат.% Ir (механическая
заточка) в насыщенных водных растворах ГПС на воздухе при разомкнутой цепи
в течение 10–12 ч. Туннельные спектры систем «модифицированный зонд — Рt-фольга»
регистрировали на воздухе, используя установку LitScan2 [10]. Базовые значения
туннельного тока составляли 0,2–1 нА, туннельного напряжения — 100–200
мВ, характерные времена квадратных импульсов напряжения — 250 мкс, длительность
интервалов между импульсами — 200 мс. Методические аспекты выбора режимов
измерений, обеспечивающих неизменность положения зонда, подробно рассмотрены
в [10]. В контрольных опытах использовали обычные зонды и Pt-фольгу, модифицированную
при помощи ГПС по аналогичной методике.
![]() Самоорганизованные монослои с характерными векторами двумерной решетки
1.2–1.5 нм на твердых подложках были ранее обнаружены методом СТМ для различных
классов ГПС и систематически исследованы методом туннельной спектроскопии
на базисной грани пирографита [11–12]. На туннельных вольт-амперных характеристиках
Itun,Utun для некоторых структурных элементов поверхностных решеток были
обнаружены участки отрицательного дифференциального сопротивления. Положения
минимумов тока коррелировали с величинами характерных потенциалов электрохимических
превращений соответствующих ГПС (восстанавливающихся, в отличие от большинства
ГПС со структурой Андерсона, только по оксометаллатным лигандам). Существование
корреляции указывает на промежуточный перенос электрона на определенную
орбиталь молекулярного кластера.
Самоорганизованные монослои с характерными векторами двумерной решетки
1.2–1.5 нм на твердых подложках были ранее обнаружены методом СТМ для различных
классов ГПС и систематически исследованы методом туннельной спектроскопии
на базисной грани пирографита [11–12]. На туннельных вольт-амперных характеристиках
Itun,Utun для некоторых структурных элементов поверхностных решеток были
обнаружены участки отрицательного дифференциального сопротивления. Положения
минимумов тока коррелировали с величинами характерных потенциалов электрохимических
превращений соответствующих ГПС (восстанавливающихся, в отличие от большинства
ГПС со структурой Андерсона, только по оксометаллатным лигандам). Существование
корреляции указывает на промежуточный перенос электрона на определенную
орбиталь молекулярного кластера.
![]() ГПС со структурой Андерсона (рис.1а) — наименее исследованный в плане адсорбции
и электрохимии класс полиоксометаллатных комплексов [9]. Благодаря октаэдрической
конфигурации центрального иона в этой структуре могут быть стабилизированы
многие гетероатомы в высоких степенях окисления, восстанавливающиеся при
более положительных потенциалах, чем оксометаллатные лиганды. При одно-
и двухэлектронном восстановлении может иметь место туннельный резонанс
с энергетическими уровнями гетероатома или смешанных молекулярных орбиталей,
находящихся в ближней окрестности геометрического центра аниона ГПС, что
обуславливает локализацию (задержку) электрона в «молекулярном резонаторе».
ГПС со структурой Андерсона (рис.1а) — наименее исследованный в плане адсорбции
и электрохимии класс полиоксометаллатных комплексов [9]. Благодаря октаэдрической
конфигурации центрального иона в этой структуре могут быть стабилизированы
многие гетероатомы в высоких степенях окисления, восстанавливающиеся при
более положительных потенциалах, чем оксометаллатные лиганды. При одно-
и двухэлектронном восстановлении может иметь место туннельный резонанс
с энергетическими уровнями гетероатома или смешанных молекулярных орбиталей,
находящихся в ближней окрестности геометрического центра аниона ГПС, что
обуславливает локализацию (задержку) электрона в «молекулярном резонаторе».
|
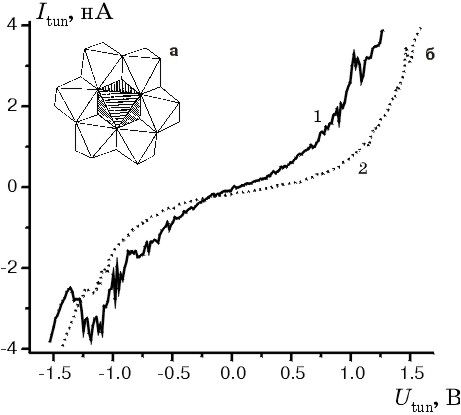
| Рис 1. Полиэдрическое изображение ГПС со структурой Андерсона: темный октаэдр — окружение гетероатома, светлые — оксомолибдатные октаэдры (а). Экспериментальные туннельные вольт-амперные характеристики при базовом токе 200 рА и базовых напряжениях 100 (1) и 600 (2) мВ (б). |
![]() Модифицирование зондов СТМ кластерами М4[PtMo6O24] приводит к возникновению
участков отрицательного дифференциального сопротивления при туннельных
напряжениях около 1 В (рис.1б). Форма этих участков зависит от базовых
величин туннельного тока и напряжения, то есть от ширины туннельного барьера:
увеличение напряжения (оно больше для кривой 2 на рис. 1б) приводит к исчезновению
эффекта. В некоторых случаях удается наблюдать на одной ветви спектра два
участка отрицательного дифференциального сопротивления.
Модифицирование зондов СТМ кластерами М4[PtMo6O24] приводит к возникновению
участков отрицательного дифференциального сопротивления при туннельных
напряжениях около 1 В (рис.1б). Форма этих участков зависит от базовых
величин туннельного тока и напряжения, то есть от ширины туннельного барьера:
увеличение напряжения (оно больше для кривой 2 на рис. 1б) приводит к исчезновению
эффекта. В некоторых случаях удается наблюдать на одной ветви спектра два
участка отрицательного дифференциального сопротивления.
![]() Туннельная проводимость, оцененная по величине dItun/dUtun в области нормального
хода спектра, близка к проводимости зазора в отсутствие ГПС (сопротивление
около 1 ГОм). Это сопоставление, однако, не вполне корректно, поскольку
введение кластера в зазор может в принципе изменить вольт- и ток- высотные
зависимости. Особенно существенным это обстоятельство становится при базовых
токах 1–2 нА, использованных в [11–12], то есть при меньшей толщине зазора
и более резких изменениях вольт- и ток-высотных спектров.
Туннельная проводимость, оцененная по величине dItun/dUtun в области нормального
хода спектра, близка к проводимости зазора в отсутствие ГПС (сопротивление
около 1 ГОм). Это сопоставление, однако, не вполне корректно, поскольку
введение кластера в зазор может в принципе изменить вольт- и ток- высотные
зависимости. Особенно существенным это обстоятельство становится при базовых
токах 1–2 нА, использованных в [11–12], то есть при меньшей толщине зазора
и более резких изменениях вольт- и ток-высотных спектров.
![]() В сравнительных экспериментах с ГПС на плоской поверхности (а не на зонде),
эффект отрицательного дифференциального сопротивления не всегда воспроизводился,
а в некоторых опытах вообще не наблюдался, что связано, вероятно, с недостаточной
степенью локальности измерений тока. При локализации ГПС на зонде его участие
в процессе переноса гарантируется вне зависимости от состояния поверхности
образца и латерального положения зонда.
В сравнительных экспериментах с ГПС на плоской поверхности (а не на зонде),
эффект отрицательного дифференциального сопротивления не всегда воспроизводился,
а в некоторых опытах вообще не наблюдался, что связано, вероятно, с недостаточной
степенью локальности измерений тока. При локализации ГПС на зонде его участие
в процессе переноса гарантируется вне зависимости от состояния поверхности
образца и латерального положения зонда.
![]() На туннельных вольт-амперных характеристиках ГПС, осажденных на базисную
грань пирографита [11–12], наиболее выражены области минимумов тока, а
при наличии ГПС на острие зонда отчетливо фиксируются последующие максимумы
или плато. Различия в условиях проведения двух обсуждаемых серий измерений,
таким образом, не сводятся лишь к разной природе исследованных ГПС и специфике
туннельно-спектроскопических режимов. Модифицированный зонд обеспечивает
преимущественное туннелирование электрона через молекулярный кластер, локализованный
на оси острия, поскольку характерные расстояния между соседними анионами
ГПС в двумерной решетке (1 нм) сопоставимы с типичными радиусами кривизны
острия (около 10 нм), и для смещенных относительно оси острия кластеров
туннельные зазоры всегда окажутся значительно большими, чем для кластера,
расположенного точно по оси. Можно, однако, констатировать, что способность
обеспечивать формирование откликов, типичных для туннельных диодов, является
общим свойством ГПС в туннельных зазорах.
На туннельных вольт-амперных характеристиках ГПС, осажденных на базисную
грань пирографита [11–12], наиболее выражены области минимумов тока, а
при наличии ГПС на острие зонда отчетливо фиксируются последующие максимумы
или плато. Различия в условиях проведения двух обсуждаемых серий измерений,
таким образом, не сводятся лишь к разной природе исследованных ГПС и специфике
туннельно-спектроскопических режимов. Модифицированный зонд обеспечивает
преимущественное туннелирование электрона через молекулярный кластер, локализованный
на оси острия, поскольку характерные расстояния между соседними анионами
ГПС в двумерной решетке (1 нм) сопоставимы с типичными радиусами кривизны
острия (около 10 нм), и для смещенных относительно оси острия кластеров
туннельные зазоры всегда окажутся значительно большими, чем для кластера,
расположенного точно по оси. Можно, однако, констатировать, что способность
обеспечивать формирование откликов, типичных для туннельных диодов, является
общим свойством ГПС в туннельных зазорах.
![]() Прямой расчет из первых принципов вольт-амперных характеристик многоатомных
молекул и, в частности, кластеров ГПС на металлической поверхности является
трудоемкой вычислительной задачей физики твердого тела и квантовой химии.
Требуется учесть зонную структуру материала подложки и зонда (т.е. энергию
Ферми, дисперсию энергии в металлах и плотности электронных состояний),
рассчитать энергетику химических связей атомов кластера и атомов поверхности
контакта, а также интегралы перекрывания молекулярных орбиталей, по которым
электрон может туннелировать.
Прямой расчет из первых принципов вольт-амперных характеристик многоатомных
молекул и, в частности, кластеров ГПС на металлической поверхности является
трудоемкой вычислительной задачей физики твердого тела и квантовой химии.
Требуется учесть зонную структуру материала подложки и зонда (т.е. энергию
Ферми, дисперсию энергии в металлах и плотности электронных состояний),
рассчитать энергетику химических связей атомов кластера и атомов поверхности
контакта, а также интегралы перекрывания молекулярных орбиталей, по которым
электрон может туннелировать.
![]() В резонансных условиях с промежуточными уровнями электрон циркулирует по
молекулярным орбиталям с временем жизни, которое оценивается величиной
обратной ширины туннельного резонанса и может на порядок и больше превышать
фемтосекундное время баллистического пролета электрона через туннельный
зазор.
В резонансных условиях с промежуточными уровнями электрон циркулирует по
молекулярным орбиталям с временем жизни, которое оценивается величиной
обратной ширины туннельного резонанса и может на порядок и больше превышать
фемтосекундное время баллистического пролета электрона через туннельный
зазор.
| На поверхности Ферми электрон обладает скоростью порядка 1нм/фс, и время пролета зазора шириной d=1 нм составляет порядка фс. |
![]() Большое время туннелирования открывает возможность неадиабатических каналов
электронно-колебательного взаимодействия и релаксации. Исходная симметрия
электронно-вырожденного состояния может спонтанно нарушаться (эффект Яна-Теллера).
Явления типа кулоновской блокады становятся существенными, когда кулоновская
энергия, зависящая от «емкости» кластера и туннельного зазора, превосходит
тепловую. В нормальных условиях кулоновской энергией, e2/C, (где e — заряд
электрона, С — емкость контакта)
Большое время туннелирования открывает возможность неадиабатических каналов
электронно-колебательного взаимодействия и релаксации. Исходная симметрия
электронно-вырожденного состояния может спонтанно нарушаться (эффект Яна-Теллера).
Явления типа кулоновской блокады становятся существенными, когда кулоновская
энергия, зависящая от «емкости» кластера и туннельного зазора, превосходит
тепловую. В нормальных условиях кулоновской энергией, e2/C, (где e — заряд
электрона, С — емкость контакта)
| Емкость острия можно оценить как |
можно пренебречь по сравнению с тепловой. Уменьшение паразитных емкостей электродов вплоть до «емкости молекулярной системы» C~10–18 Ф обеспечивает возможность проявления кулоновской блокады даже при комнатной температуре. Помимо этого, из-за квантовой интерференции различных путей переноса по молекулярным орбиталям возможны антирезонансы туннельной прозрачности. Подробный количественный анализ когерентных и некогерентных явлений в туннельной спектроскопии ГПС требует специальной разработки сложных теоретических моделей.
![]() На данном этапе для качественного прогнозирования условий реализации эффектов
отрицательного дифференциального сопротивления целесообразно рассмотреть
резонансное туннелирование в рамках одномерной модели, в которой роль промежуточных
уровней молекулярного кластера играют виртуальные уровни эффективной квантовой
ямы. Так как типичное сопротивление туннельного контакта порядка 1 ГОм
много больше квантового сопротивления,
На данном этапе для качественного прогнозирования условий реализации эффектов
отрицательного дифференциального сопротивления целесообразно рассмотреть
резонансное туннелирование в рамках одномерной модели, в которой роль промежуточных
уровней молекулярного кластера играют виртуальные уровни эффективной квантовой
ямы. Так как типичное сопротивление туннельного контакта порядка 1 ГОм
много больше квантового сопротивления, ![]() кОм, где
кОм, где ![]() — постоянная Планка,
то обеспечиваются необходимые и достаточные условия для одноэлектронного
туннелирования. В этих условиях подгоночные параметры служат для определения
глубины и ширины ямы, а также характеристики несимметричного расположения
ямы в туннельном контакте. Менее свободными величинами являются температура
и энергии Ферми электронов, ширины запрещенных зон, обусловленные периодическими
потенциалами в объеме металла и в двумерных поверхностных слоях. «Условные»
зоны проводимости введены с целью имитировать особенности электронной плотности
в глубине металла и на берегах туннельного барьера.
— постоянная Планка,
то обеспечиваются необходимые и достаточные условия для одноэлектронного
туннелирования. В этих условиях подгоночные параметры служат для определения
глубины и ширины ямы, а также характеристики несимметричного расположения
ямы в туннельном контакте. Менее свободными величинами являются температура
и энергии Ферми электронов, ширины запрещенных зон, обусловленные периодическими
потенциалами в объеме металла и в двумерных поверхностных слоях. «Условные»
зоны проводимости введены с целью имитировать особенности электронной плотности
в глубине металла и на берегах туннельного барьера.
![]() Электроны металла в первом приближении являются плоскими блоховскими волнами.
Известно, что представление о плоских волнах более оправдано на границах
элементарных ячеек кристалла (вдали от центров остова), и потому в пограничных
явлениях для оценки туннельного тока можно ограничиться упрощенной картиной
электронного резервуара в виде идеального газа. Мы рассмотрим модель почти
свободных электронов, в которой закон дисперсии
Электроны металла в первом приближении являются плоскими блоховскими волнами.
Известно, что представление о плоских волнах более оправдано на границах
элементарных ячеек кристалла (вдали от центров остова), и потому в пограничных
явлениях для оценки туннельного тока можно ограничиться упрощенной картиной
электронного резервуара в виде идеального газа. Мы рассмотрим модель почти
свободных электронов, в которой закон дисперсии ![]() задается моделью Кронига-Пенни
кристалла в пределе Дираковской решетки, где Vgap характеризует величину
периодического потенциала, a — постоянная решетки, m — масса электрона. Туннельный ток
задается моделью Кронига-Пенни
кристалла в пределе Дираковской решетки, где Vgap характеризует величину
периодического потенциала, a — постоянная решетки, m — масса электрона. Туннельный ток
| (1) |
определяется как полный поток прошедших через барьер электронов, ![]() ,
, ![]() —
волновая функция электрона и ее производная по координате. Угловые скобки
обозначают среднее по распределению Ферми f (Eq) в начальном электронном
резервуаре с учетом конечных состояний (1–f(Eq)), которые допускаются принципом
Паули (
—
волновая функция электрона и ее производная по координате. Угловые скобки
обозначают среднее по распределению Ферми f (Eq) в начальном электронном
резервуаре с учетом конечных состояний (1–f(Eq)), которые допускаются принципом
Паули (![]() — энергия электрона с волновым вектором q). Для вычисления прозрачности
туннельного барьера T(Eq) необходимо точно численно решить уравнение Шредингера
для волновой функции
— энергия электрона с волновым вектором q). Для вычисления прозрачности
туннельного барьера T(Eq) необходимо точно численно решить уравнение Шредингера
для волновой функции
| (2) |
и найти прошедшую волну с волновым вектором ![]() . Изначально падает плоская
волна с потоком
. Изначально падает плоская
волна с потоком ![]() ,
,
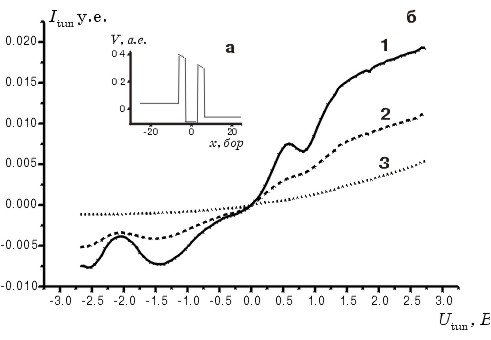
которая перед барьером образует стоячую волну. Барьер обладает прозрачностью, зависящей от энергии электрона Eq (его скорости n) и приложенного потенциала U между берегами. Схематические графики потенциальной энергии V(x) металла и молекулярного кластера приведены на рис 2а. Спектр резонансного туннелирования T(Eq) (рис.3а) и разность распределения Ферми в берегах барьера (рис.3б) позволяют рассчитать электронный ток по формуле (1), принимающей вид обобщенной формулы Ландауэра [13],
| (3) |
в которой сумма берется по разрешенным состояниям в зонах Бриллюэна. Представление (3) аналогично выражению для контура неоднородно уширенной спектральной линии в оптической спектроскопии. Узкие однородные линии резонансного туннелирования, давая вклад в полный ток, могут оказаться неразрешенными в металле из-за широких зон проводимости (порядка 5 эВ) и гладкой зависимости плотности состояний от энергии. Однако в сплавах из-за примесных состояний в узких запрещенных зонах реализуются как пики, так и провалы плотности состояний. Для достижения качественного согласия с экспериментом в этой модели нужно выбрать щель порядка десятых эВ, которая скорее характерна для полупроводников, чем для металлов
| Следует иметь ввиду, что зонная структура металла подложки и иглы при туннелировании проявляется совершенно иначе, чем в «объемных» свойствах металла, поскольку процесс туннелирования чувствителен к нормальной компоненте импульса электрона значительно сильнее, чем к тангенциальным по отношению к поверхности. Вероятность туннелирования определяется дисперсией электрона не во всем пространстве квазиимпульсов, а лишь в узкой окрестности «прокола» фазового пространства в направлении туннелирования. Специфика этого явления нуждается в специальном исследовании, здесь ограничимся замечанием о том, что под щелями в спектре электрона имеются ввиду на самом деле одномерные срезы (проколы) энергетических поверхностей в пространстве обратной решетки. Существование таких щелей шириной 0,5–1 эВ для платины согласуется с расчетами [14]. |
 |
|
Рис 2. Схематика потенциальных ям металла и квантовой ямы, отвечающей
молекулярному кластеру на поверхности зонда СТМ (а). Ширина зазора –12.56
Бор, ширина ямы –6.28 Бор, потенциал ямы ниже дна валентной зоны на –2.35
эВ. Работа выхода и энергия Ферми Ef около 4 эВ, условные запрещенные
зоны в спектре — около 0.5 эВ. Рассчитанные вольт-амперные характеристики туннельного перехода для смещенных положений (в борах) ямы относительно центра зазора (б): 1 – (0), 2 – (1), 3 – (2). Характерная для диодов однонаправленная проводимость обусловлена асимметрией нашего модельного потенциала при разных знаках приложенного напряжения, которое дает разную работу выхода с разных сторон туннельного зазора. Вопрос об условиях возникновения асимметрии на экспериментальной вольтамперной характеристике будет исследован в дальнейшем специально. |
![]() Чем длиннее туннельная траектория, тем уже виртуальный уровень и тем
острее могут быть пики тока, при условии что квантовая яма расположена
симметрично. Сдвиг ямы от центра траектории приводит к падению амплитуды
туннельных резонансов (рис.2б).
Чем длиннее туннельная траектория, тем уже виртуальный уровень и тем
острее могут быть пики тока, при условии что квантовая яма расположена
симметрично. Сдвиг ямы от центра траектории приводит к падению амплитуды
туннельных резонансов (рис.2б).
| При выборе параметров модели мы ориентировались на случай ГПС со структурой Андерсона, то есть полагали толщину одного из двух туннельных зазоров равной размеру октаэдра лиганда, а второго — такой же (если модифицированный зонд подведен вплотную к плоскому образцу) или большей (в случае суммирования с воздушным зазором). Расстояние между зазорами являлось близким к характерному размеру центрального иона (0,1–0,2 нм). |
![]() Рассчитанные вольт-амперные характеристики качественно воспроизводят экспериментальные
тенденции (наличие областей отрицательного дифференциального сопротивления
на обоих ветвях туннельных спектров, размывание резонансов при отодвигании
зонда от поверхности путем увеличения базового напряжения). Рельеф туннельной
прозрачности как функции энергии (Е) и приложенного напряжения (U) (рис.
3а) имеет вид долины с узким резонансным хребтом (единичной амплитуды),
проходящим вблизи энергии Ферми, с выходом на холмистое плато, лежащее
в области непрерывного спектра, т.е. выше работы выхода металла. Линии
уровня сгущаются вблизи туннельного резонанса. Наклон хребта характеризует
сдвиг энергетического уровня в потенциальном поле. При положительном потенциале
возможен только один резонанс, а при отрицательных — два, т.к. яма становится
более глубокой. Второй резонанс образуется выше границы заполнения электронного
резервуара и не влияет на электронный перенос. Холмистое плато соответствует
надбарьерным резонансам при еще более высоких энергиях, не дающим вклада
в туннельный ток при напряжениях порядка 1–2 В (они также не перекрываются
с электронным распределением, ограниченным энергией Ферми).
Рассчитанные вольт-амперные характеристики качественно воспроизводят экспериментальные
тенденции (наличие областей отрицательного дифференциального сопротивления
на обоих ветвях туннельных спектров, размывание резонансов при отодвигании
зонда от поверхности путем увеличения базового напряжения). Рельеф туннельной
прозрачности как функции энергии (Е) и приложенного напряжения (U) (рис.
3а) имеет вид долины с узким резонансным хребтом (единичной амплитуды),
проходящим вблизи энергии Ферми, с выходом на холмистое плато, лежащее
в области непрерывного спектра, т.е. выше работы выхода металла. Линии
уровня сгущаются вблизи туннельного резонанса. Наклон хребта характеризует
сдвиг энергетического уровня в потенциальном поле. При положительном потенциале
возможен только один резонанс, а при отрицательных — два, т.к. яма становится
более глубокой. Второй резонанс образуется выше границы заполнения электронного
резервуара и не влияет на электронный перенос. Холмистое плато соответствует
надбарьерным резонансам при еще более высоких энергиях, не дающим вклада
в туннельный ток при напряжениях порядка 1–2 В (они также не перекрываются
с электронным распределением, ограниченным энергией Ферми).
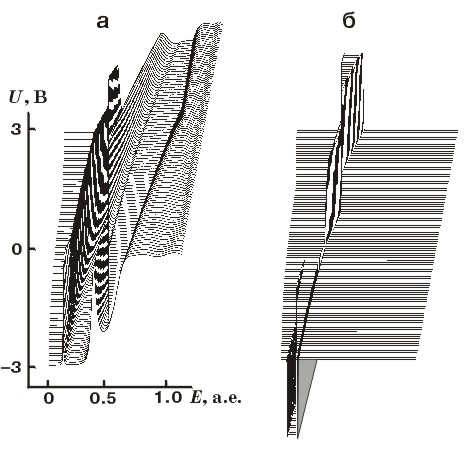 |
| Рис. 3. Контурная карта туннельной прозрачности (четыре эквидистантных уровня) (а). Контурная карта распределения f(Ek+eU)(1–f(Ek)) электронов модели Кронига-Пенни (б). Сплошными линиями рисуются два эквидистантных уровня распределения для положительных напряжений U. Пунктирными линиями — два эквидистантных уровня для отрицательных U. |
![]() Х-образная контурная карта распределения f(Ek+eU)(1–f(Ek)) (рис. 3б) учитывает
принцип запрета Паули для переноса между электронными резервуарами и дополняет
картину формирования туннельной спектрограммы. С увеличением положительного
потенциала запрещенная щель между валентной зоной и зоной проводимости
синхронно сдвигается, образуя наклонную полоску в верхней части рис.3б.
Пересечение этой щели в распределении электронов и линии резонансной прозрачности
обеспечивает падение тока и формирует область отрицательного дифференциального
сопротивления. Аналогичная картина имеет место и при отрицательных потенциалах
с той лишь разницей, что запрещенная щель проходит вертикально (в нижней
части рис.3б), т.к. потенциал эмитирующего электроны резервуара не сдвигается.
Х-образная контурная карта распределения f(Ek+eU)(1–f(Ek)) (рис. 3б) учитывает
принцип запрета Паули для переноса между электронными резервуарами и дополняет
картину формирования туннельной спектрограммы. С увеличением положительного
потенциала запрещенная щель между валентной зоной и зоной проводимости
синхронно сдвигается, образуя наклонную полоску в верхней части рис.3б.
Пересечение этой щели в распределении электронов и линии резонансной прозрачности
обеспечивает падение тока и формирует область отрицательного дифференциального
сопротивления. Аналогичная картина имеет место и при отрицательных потенциалах
с той лишь разницей, что запрещенная щель проходит вертикально (в нижней
части рис.3б), т.к. потенциал эмитирующего электроны резервуара не сдвигается.
![]() Эксперименты в конфигурации СТМ и модельные расчеты туннельных резонансов
применимы для анализа самых разных, в том числе органических молекул [15].
Туннельная спектроскопия резонансных уровней высокого разрешения может
быть реализована на принципах, заимствованных из оптической нелинейной
спектроскопии. Наш подход обобщается для задач когерентного и квантового
управления туннельными токами. Наличие дискретных молекулярных состояний
позволяет использовать резонансное оптическое поле на связно-связанных
переходах для усиления (ослабления) туннельной прозрачности. Когерентное
управление туннельными переходами важно c прикладной точки зрения для разработки
схем оптических транзисторов и оптоэлектронных преобразователей. Фундаментальный
интерес представляет решение обратных задач туннельной спектроскопии: установление
потенциалов нанокластера и зонной структуры электронного резервуара.
Эксперименты в конфигурации СТМ и модельные расчеты туннельных резонансов
применимы для анализа самых разных, в том числе органических молекул [15].
Туннельная спектроскопия резонансных уровней высокого разрешения может
быть реализована на принципах, заимствованных из оптической нелинейной
спектроскопии. Наш подход обобщается для задач когерентного и квантового
управления туннельными токами. Наличие дискретных молекулярных состояний
позволяет использовать резонансное оптическое поле на связно-связанных
переходах для усиления (ослабления) туннельной прозрачности. Когерентное
управление туннельными переходами важно c прикладной точки зрения для разработки
схем оптических транзисторов и оптоэлектронных преобразователей. Фундаментальный
интерес представляет решение обратных задач туннельной спектроскопии: установление
потенциалов нанокластера и зонной структуры электронного резервуара.
![]() Выражаем свою признательность А.В.Данилову за полезное обсуждение. Работа
выполнена при поддержке РФФИ, проект 96–02–17782а.
Выражаем свою признательность А.В.Данилову за полезное обсуждение. Работа
выполнена при поддержке РФФИ, проект 96–02–17782а.